Hai đường thẳng vuông góc lớp 11

Hai đường thẳng vuông góc lớp 11

Hôm nay  sẽ giúp các bạn hiểu rõ hơn về lý thuyết hai đường thẳng vuông góc toán 11!

I. Lý thuyết

1. Định nghĩa

Hai đường thẳng bất kỳ khi mà chúng tạo với nhau một góc 90 độ thì ta nói hai đường thẳng đó là vuông góc với nhau.

Ký hiệu: a ⊥ b. Ta nói a vuông góc với b, hay a và b là hai đường vuông góc.

2. Nhận xét

- Đối với hai đường vuông góc a và b ta có lần lượt \(\overrightarrow {u},\overrightarrow {v}\)là hai vecto có hướng tương ứng, khi đó ta có \(\overrightarrow {u}.\overrightarrow {v}=\overrightarrow {0}\)

- Xét hai đường thẳng đã cho là song song, nếu một đường thẳng vuông góc với một đường thẳng này thì chắc chắn sẽ bắc cầu vuông góc với đường thẳng còn lại.

- Hai đường thẳng sẽ có tính chất là chéo nhau hoặc chúng cắt nhau khi vuông góc.

Trắc nghiệm hai đường thẳng vuông góc lớp 11

II. Các dạng bài tập về 2 đường thẳng vuông góc

1. Dạng 1: Tìm góc giữa hai đường thẳng.

Phương pháp: Ta có hai cách cơ bản để tính góc giữa hai đường thẳng như sau:

- Cách 1:

+ Tìm góc giữa hai đường a và b trong không gian bằng cách lấy một điểm O thích hợp (điểm O này sẽ nằm trên một đường bất kỳ có thể là a hoặc b).

+ Từ điển O ta lần lượt tạo ra các đường a' và b' sao cho a'//a và b'//b. Vì vậy góc giữa hai đường a' và b' sẽ chính bằng góc giữa hai đường thẳng a và b ban đầu.

+ Để tính được góc này ta áp dụng định lý cosin như sau:

\(cosA=\dfrac{b^2+c^2-a^2}{2bc}\).

- Cách 2:

+ Tìm hai vecto chỉ phương \(\overrightarrow {u_1},\overrightarrow {u_2}\) lần lượt ứng với hai đường thẳng a và b.

+ Khi đó ta có góc giữa hai đường thẳng a và b sẽ được xác định bằng công thức sau: \(cos(a,b)=\dfrac{|\overrightarrow {u_1}.\overrightarrow {u_2}|}{|\overrightarrow {u_1}|.|\overrightarrow {u_2}|}\).

Để tính \(\overrightarrow {u_1},\overrightarrow {u_2},|\overrightarrow {u_1}|,|\overrightarrow {u_2}|\) ta lần lượt chọn ba vecto không đồng phẳng \(\overrightarrow {m},\overrightarrow {n},\overrightarrow {p}\)sao cho có thể tính được độ dài và góc giữa chúng, sau đó biến đổi ngược lại biểu thị các vecto \(\overrightarrow {u_1},\overrightarrow {u_2}\)  qua các vecto \(\overrightarrow {m},\overrightarrow {n},\overrightarrow {p}\)rồi thực hiện các phép tính toán như thông thường.

2. Dạng 2: Dùng tích vô hướng để chứng minh hai đường thẳng vuông góc.

Phương pháp: Đối với  hai đường thẳng bất kỳ a và b ta lấy hai vecto  \(\overrightarrow {u_1},\overrightarrow {u_2}\) lần lượt ứng với hai vecto ban đầu. Để a vuông góc với b ta chứng minh đẳng thức \(\overrightarrow {u}.\overrightarrow {v}=\overrightarrow {0}\).

III. Bài tập vận dụng

Bài 1: 

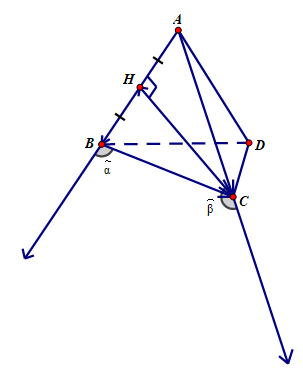
Cho tứ diện đều ABCD có H là trung điểm của cạnh AB. Hãy tính góc giữa các cặp vecto sau đây:

a) \(\overrightarrow {AB} \ và \ \overrightarrow { BC}\)

b) \(\overrightarrow {CH} \ và \ \overrightarrow {AC}\)

Lời giải

Tứ diện ABCD đều có các mặt là tam giác đều

a) Góc giữa (\(\overrightarrow {AB} \ và \ \overrightarrow { BC}\) là góc α và \(\widehatα = 180^o- 60^o = 120^o\)

b) Góc giữa \(\overrightarrow {CH} \ và \ \overrightarrow {AC}\) là góc β

H là trung điểm cạnh AB của tam giác đều ABC nên CH vừa là trung tuyến vừa là đường cao nên CH ⊥ AB

Xét tam giác vuông ACH tại H có \(\widehat{ACH} + \widehat{HAC} = 90^o ⇒ \widehat{ACH} = 90^o - 60^o = 30^o\)

Nên \(\widehatβ = 180^o- 30^o= 150^o\)

Bài 2: 

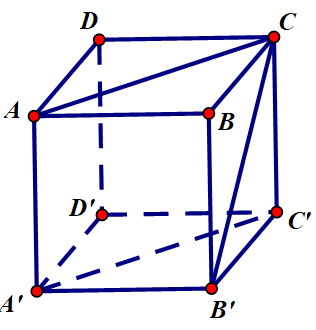
Cho hình lập phương ABCD.A’B’C’D’. Tính góc giữa các cặp đường thẳng sau đây:

a) AB và B’C’

b) AC và B’C’

c) A’C’ và B’C

Lời giải

a) Góc giữa AB và B’C’ = góc giữa AB và BC (vì B’C’//BC)

⇒ Góc giữa AB và B’C’ = \(\widehat{ABC} = 90^o\)

b) Góc giữa AC và B’C’ = góc giữa AC và BC (vì B’C’//BC)

⇒ Góc giữa AC và B’C’ = \(\widehat{ACB} = 45^o\)

c) Góc giữa A’C’ và B’C = góc giữa AC và B’C (vì A’C’//AC)

ΔACB’ đều vì AC = B’C = AB’ (đường chéo của các hình vuông bằng nhau)

⇒ Góc giữa A’C’ và B’C = \(\widehat{ACB'} = 60^o\)

Hy vọng với những kiến thức bổ ích mà muốn chia sẻ với các bạn về các dạng bài tập về hai đường thẳng vuông góc thường gặp. Chúc các bạn có những giờ học bổ ích!