Đề kiểm tra 15 phút - Đề số 3 - Bài 5, 6 - Chương 1 - Hình học 7
Tóm tắt bài
Đề bài
Bài 1: Cho tam giác ABC. Chứng minh rằng: nếu đường thẳng d song song với BC thì d sẽ cắt các đường thẳng AB và AC.
Bài 2: Cho hình vẽ biết a // b và một góc tù tại A bằng 130o. Tính góc nhọn tạo bởi c và b.

Hướng dẫn giải
Bài 1:
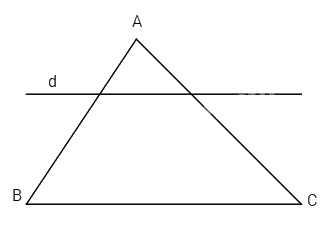
Giả sử d không cắt AB \( \Rightarrow AB//d,\) lại có BC // d.
Như vậy qua một điểm B có AB và BC cùng song song với d. Trái với tiên đè Ơclit. Vậy d cắt AB.
Chứng minh tương tự ta có d cắt AC.
Bài 2: Gọi B là giao điểm của c và b. (xem hình vẽ).
Ta có \( \Rightarrow \widehat {{B_1}} = {180^o} - \widehat {{B_2}} \)\(\,= {180^o} - {130^o} = {50^o}.\)
\(\widehat {{B_2}} = \widehat A = {130^o}\) (cặp góc so le trong) mà \(\widehat {{B_2}} = \widehat {{B_1}} = {180^o}\) (cặp góc kề bù) \( \Rightarrow \widehat {{B_1}} = {180^o} - \widehat {{B_2}} = {180^o} - {130^o}\)\(\, = {50^o}.\)
Vậy số đo của góc nhọn tạo bới c và b là 50o.
Copyright © 2021 HOCTAP247
