Trang chủ
Lớp 7
Toán Lớp 7 SGK Cũ
Bài 7. Định lí Py-ta-go
Đề kiểm tra 15 phút - Đề số 4 - Bài 7, 8 - Chương 2 - Hình học 7
Đề kiểm tra 15 phút - Đề số 4 - Bài 7, 8 - Chương 2 - Hình học 7
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Cho tam giác ABC vuông ở A có \(\dfrac{{AB}}{ {AC}} = \dfrac{8 }{ {15}}\) và BC = 51cm.
a) Tính AB, AC.
b) Tính diện tích tam giác ABC
Hướng dẫn giải
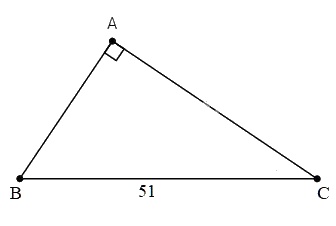
a) Ta có \(\dfrac{{AB} }{{AC}} = \dfrac{8 }{{15}} \Rightarrow \dfrac{{AB}}{ 8} = \dfrac{{AC} }{ {15}}\)
\( \Rightarrow \dfrac{{A{B^2}} }{ {64}} = \dfrac{{A{C^2}} }{ {225}} = \dfrac{{A{B^2} + A{C^2}} }{ {64 + 225}} \)\(\,=\dfrac {{B{C^2}} }{ {289}} =\dfrac {{{{51}^2}} }{ {289}} = 9.\)
Do đó \(A{B^2} = 64.9 = 576 \Rightarrow AB = 24\,(cm)\)
\(A{C^2} = 225.9 = 2025\)\(\, \Rightarrow AC = 45\,(cm).\)
b) Gọi S là diện tích tam giác ABC ta có
\(S = \dfrac{1 }{ 2}AB.AC\)
\( \;\;\;= \dfrac{1 }{ 2}.24.45 = 540\,(c{m^2})\)
Copyright © 2021 HOCTAP247
