Giải bài 3 trang 56 - Sách giáo khoa Toán 7 tập 2

Đề bài

Cho tam giác ABC với góc A = 100\(^0\), góc B = 40\(^0\).

a) Tìm cạnh lớn nhất của tam giác ABC.

b) Tam giác ABC là tam giác gì?

Hướng dẫn giải

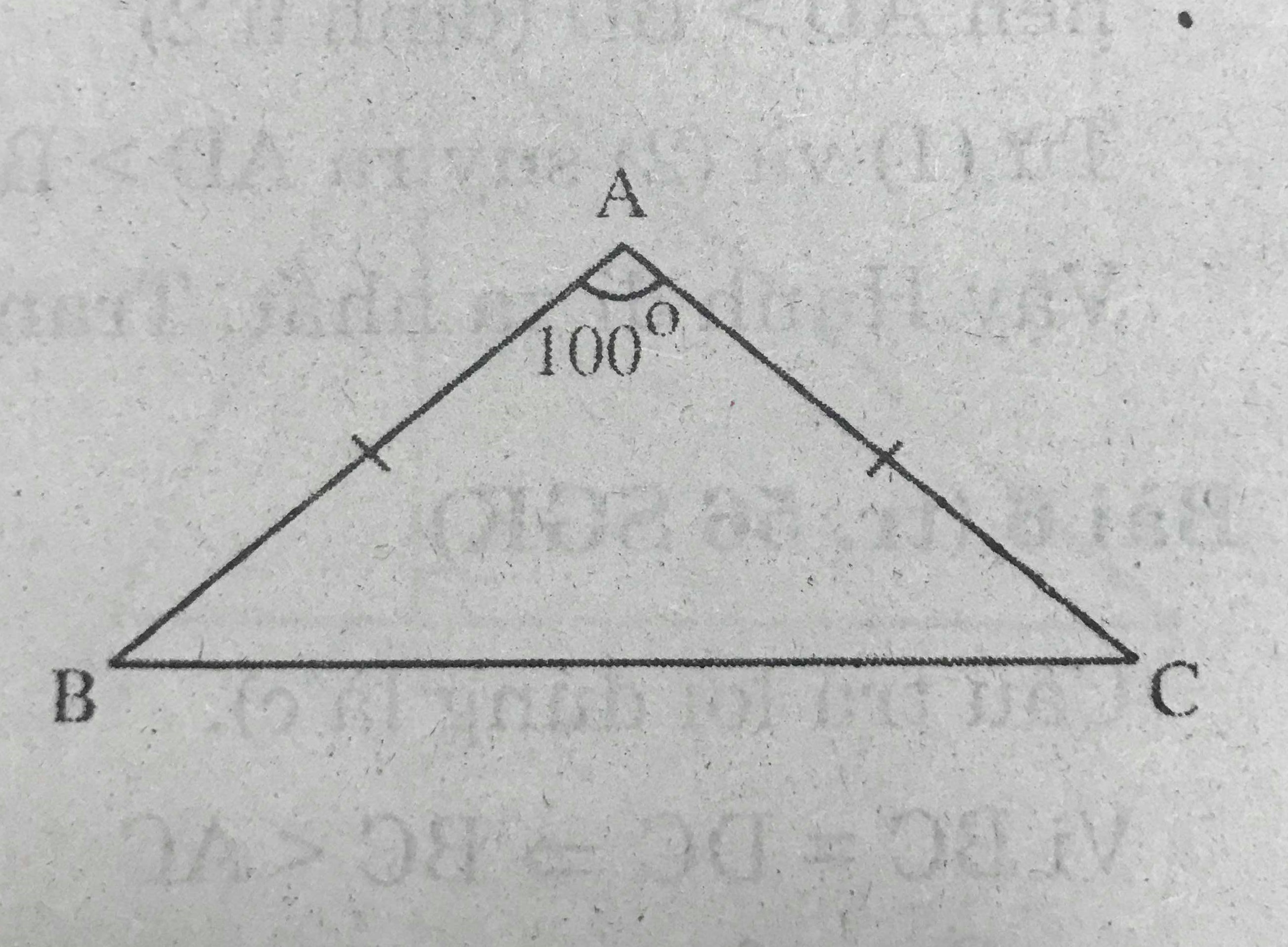
a) \(\widehat{A}=100^0\) là góc tù nên là góc lớn nhất trong \(\triangle\)ABC (tổng ba góc trong một tam giác bằng 180\(^0\))

Do đó cạnh BC là cạnh lớn nhất của \(\triangle\)ABC (cạnh đối diện của góc lớn nhất thì lớn nhất)

b) \(\triangle\)ABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)

=> \(\widehat{C}=180^0-\widehat{A}-\widehat{B}=180^0-100^0-40^0=40^0\)

\(\triangle\)ABC có \(​​\widehat{B}=\widehat{C}(=40^0)\) nên là tam giác cân.