Giải bài 7 trang 56 - Sách giáo khoa Toán 7 tập 2

Đề bài

Một cách chứng minh khác của định lí 1:

Cho tam giác ABC với AC > AB. Trên tia AC, lấy điểm B' sao cho AB' = AB.

a) Hãy so sánh góc ABC với góc ABB'.

b) Hãy so sánh góc ABB' với góc AB'B.

c) Hãy so sánh góc AB'B với góc ACB.

Từ đó suy ra \(\widehat{ABC}<\widehat{ACB}\)

Hướng dẫn giải

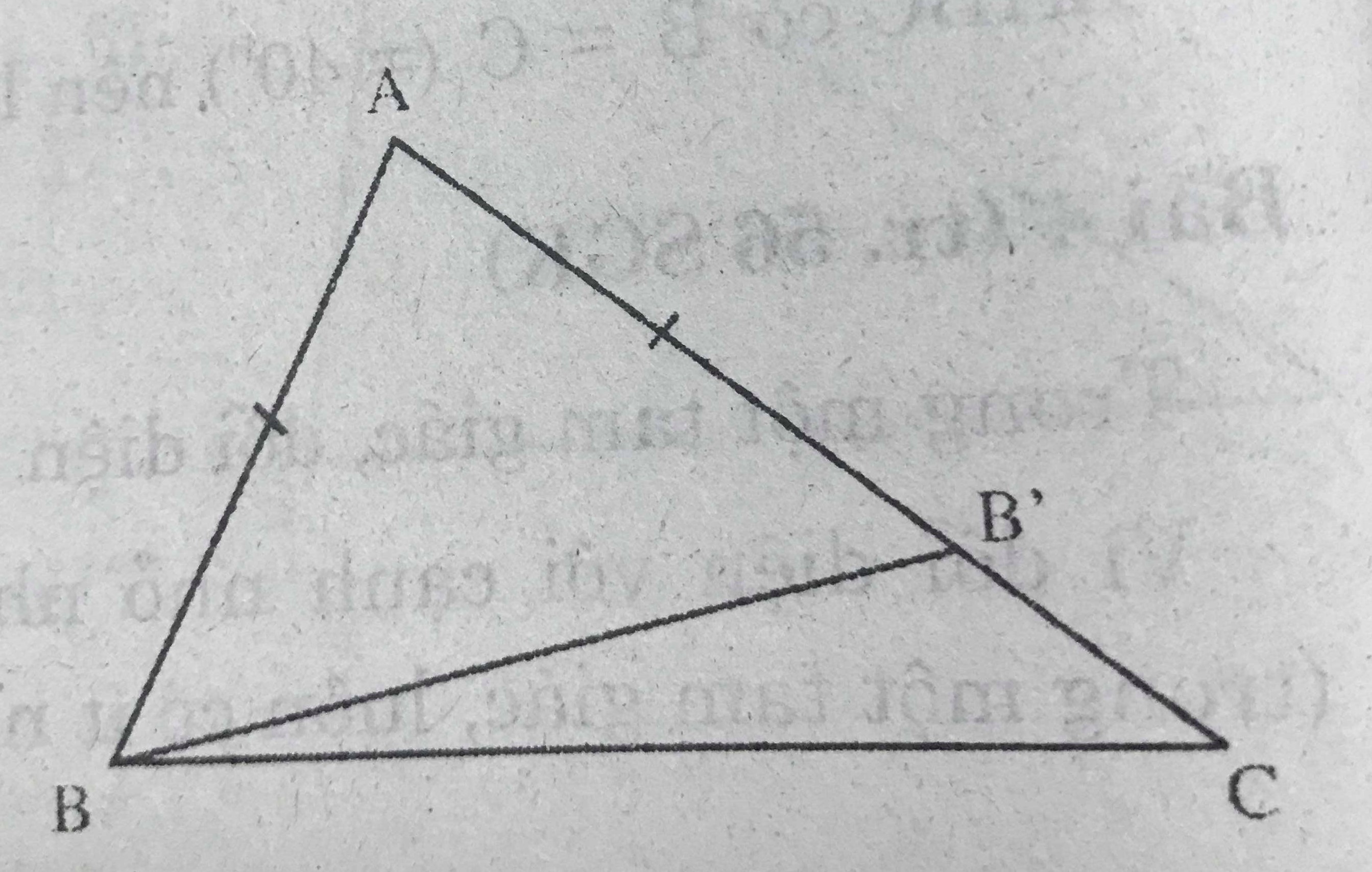
a) Ta có \(\widehat{ABC}=\widehat{ABB'}+\widehat{B'BC}\) nên \(\widehat{ABC}>\widehat{ABB'}\)   (1)

b) \(\triangle ABB'\) có AB = AB' nên là tam giác cân ở A.

Do đó \(\widehat{ABB'}=\widehat{AB'B}\)        (2)

c) \(\widehat{AB'B}\) là góc ngoài của \(\triangle \widehat{B'BC}\) nên \(\widehat{AB'B}>\widehat{BCB'}\) (góc ngoài của tam giác luôn lớn hơn hai góc trong không kề với nó).

Tức là \(\widehat{AB'B}=\widehat{ACB}\) (3)

Từ (1) (2) (3) suy ra \(​​\widehat{ABC}>\widehat{ACB}\)