Một bản mặt song song có bề dày 6cm, chiết suất n=1,5 được đặt trong không khí.

* Hướng dẫn giải

Ta có hình vẽ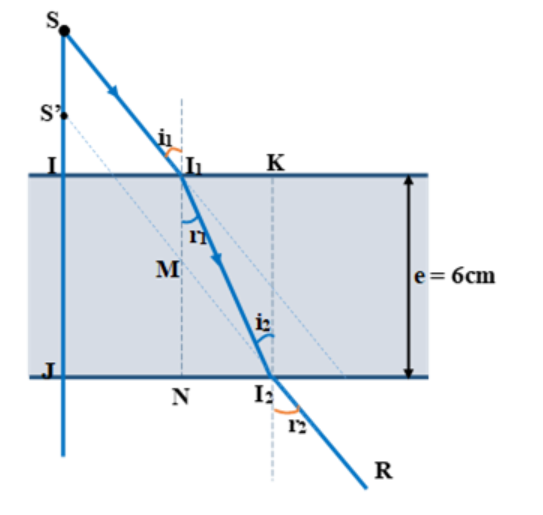

Ta thấy tia ló ${I}_2{R}$ song song với tia tới ${S}{I}_1$, giao của đường kéo dài của tia ${I}_2{R}$ cắt tia sáng SJ tại S', S' là ảnh của S qua bản mặt.
Tứ giác ${S}{S}'{M}{I}_1$ là hình bình hành
$→{S}{S}'={I}_1{M}$
Xét 2 tam giác vuông ${M}{N}{I}_2$ và ${I}_1{N}{I}_2$ ta có:
$\begin{array}{l} \mathrm{NI}_{2}=\mathrm{I}_{1} \mathrm{~N} \text { .tanr } 1=\mathrm{MN} \cdot \text { tani } 1 \text { (do góc } \left.\mathrm{NMI}_{2}=\mathrm{i}_{1}\right) \\\rightarrow \mathrm{MN}=\mathrm{I}_{1} \mathrm{~N} \cdot \frac{\mathrm{t} \text { anr }_{1}}{\tan \mathrm{i}_{1}}\end{array}$
Vì ta đang xét góc tới ${i}_1$ rất nhỏ nên ${r}_1$ cũng rất nhỏ
=>$\begin{array}{l}\rightarrow \tan i_{1} \approx \sin i_{1} \text { và tanr }_{1} \approx \sin r_{1} \\\rightarrow M N=I_{1} N \cdot \frac{\tan r_{1}}{\tan i_{1}} \approx e \cdot \frac{\sin r_{1}}{\sin i_{1}}=e \cdot \frac{1}{n}\end{array}$
(theo định luật khúc xạ tại ${I}_1$: ${sin}{i}_1={n}.{sin}{r}_1$)
→Khoảng cách giữa vật và ảnh là:
$SS'=I_1M=I_1N-MN= e - e/n=6-6 /1,5=2$ cm\end{array}