Trang chủ
Đề thi & kiểm tra
Lớp 11
Vật lý
Trắc nghiệm Vật lý 11 bài 26: Khúc xạ ánh sáng
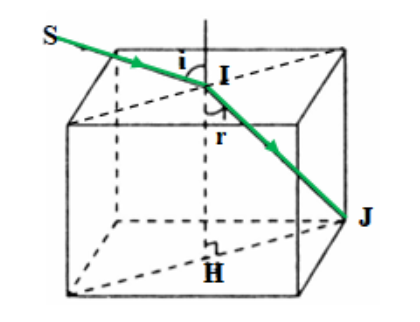
Một tia sáng được chiếu điến giữa của mặt trên...
Một tia sáng được chiếu điến giữa của mặt trên của khối lập phương trong suốt,
Câu hỏi :
Một tia sáng được chiếu điến giữa của mặt trên của khối lập phương trong suốt, chiết suất n = 1,50 (hình vẽ). Tìm góc tới i lớn nhất để tia khúc xạ vào trong khối còn gặp mặt đáy của khối.
A. ${45}^0$
B. ${60}^0$
C. ${54}^0$
D. ${43}^0$
* Đáp án
B
* Hướng dẫn giải
Gọi a là cạnh của khối lập phương. Áp dụng định luật khúc xạ ở mặt trên ta có: sini = n.sinr (1)Điều kiện góc tới ${i}={i}_{{m}{a}{x}}$ để tia khúc xạ vào trong khối còn gặp mặt đáp của khối là tia khúc xạ trùng với phương IJ với J là đỉnh của hình hộp như hình vẽ: ${r}={r}_{{m}{a}_x}$
Trong đó: $IH= a; HJ=\dfrac{a\sqrt{2}}{2} \rightarrow IJ=\sqrt{IH^2 +HJ^2}=\sqrt{{a}^{2}+\left(\frac{\mathrm{a} \sqrt{2}}{2}\right)^{2}}=a.\sqrt{\dfrac{3}{2}}$
Do đó:
$ \sin r_{\max }=\dfrac{H J}{I J}=\frac{\frac{a}{\sqrt{2}}}{a \cdot\sqrt{\frac{3}{2}}}=\frac{1}{\sqrt{3}}$
Từ (1) và (2) suy ra
$sini_{max }=1,5\cdot \dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{2} \rightarrow i_{max }=60$
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Vật lý 11 bài 26: Khúc xạ ánh sáng
Số câu hỏi: 20
Copyright © 2021 HOCTAP247
