Trang chủ
Đề thi & kiểm tra
Lớp 11
Vật lý
Trắc nghiệm Vật lý 11 bài 28: Lăng kính
Một lăng kính có chiết suất n=sqrt2. Chiếu một tia...
Một lăng kính có chiết suất n=sqrt2. Chiếu một tia sáng đơn sắc vào mặt bên của
Câu hỏi :
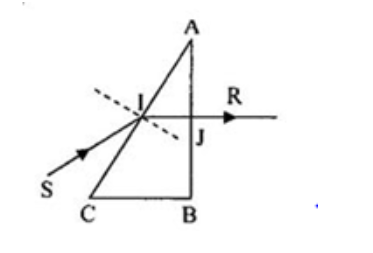
Một lăng kính có chiết suất ${n}{=}\sqrt{2}$. Chiếu một tia sáng đơn sắc vào mặt bên của lăng kính góc tới ${i}{=}45^0$, tia ló ra khỏi lăng kính vuông góc với mặt bên thứ 2 như hình vẽ. Góc chiết quang A của lăng kính:
A. $45^0$
B. $30^0$
C. $60^0$
D. $70^0$
* Đáp án
B
* Hướng dẫn giải
Áp dụng định luật khúc xạ ánh sáng tại điểm tới I của mặt thứ nhất, ta có:${sin}{i}_1{=}{n}{{sinr}}_1{↔}{sin}45{=}{\sqrt{2}}{{sinr}}_1{→}{{sinr}}_1{=}\dfrac12{→}{r}_1{=}30^0$
Vì tia ló ra khỏi mặt thứ 2 đi vuông góc nên: ${i}_2{=}0{→}{r}_2{=}0$
Ta có: ${A}{=}{r}_1{+}{r}_2{=}30{+}0{=}30^0$
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Vật lý 11 bài 28: Lăng kính
Số câu hỏi: 38
Copyright © 2021 HOCTAP247
