Trang chủ
Đề thi & kiểm tra
Lớp 11
Vật lý
Trắc nghiệm Vật lý 11 bài 28: Lăng kính
Chiếu một tia sáng SI đến vuông góc với màn...
Chiếu một tia sáng SI đến vuông góc với màn E tại I. Trên đường đi của tia sáng,
Câu hỏi :
Chiếu một tia sáng SI đến vuông góc với màn E tại I. Trên đường đi của tia sáng, người ta đặt tại đỉnh A của một lăng kính thủy tinh có góc chiết quang ${A}{=}5^0$, chiết suất n = 1,5 sao cho SI vuông góc với mặt phân giác của góc chiết quang A, tia sáng ló đến màn E tại điểm J. Đoạn IJ = ?
Biết rằng màn E đặt cách đỉnh A của lăng kính một khoảng 1m.
A. $8,72{c}{m}$
B. $2,5{m}$
C. $2,5{c}{m}$
D. $4,36{c}{m}$
* Đáp án
D
* Hướng dẫn giải
Ta có hình vẽ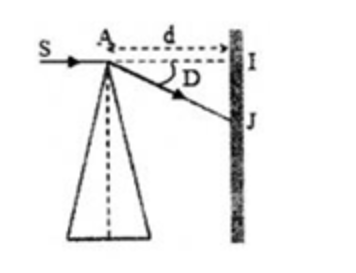
Vì góc chiết quang nhỏ nên ta dễ suy ra công thức tính góc lệch giữa tia tới và tia ló là: ${D}{=}{(}{n}{-}1{)}{A}$
Từ hình vẽ, ta có: ${tan}{D}{=}\dfrac{{IJ}}{{A}{I}}$
Vì A nhỏ, nên D nhỏ
Ta có: ${tan}{D}{≈}{D}$
${↔}{(}{n}{-}1{)}{A}{=}\dfrac{{I}{J}}{{A}{I}}{=}\dfrac{{IJ}}{d}$
${→}{I}{{J}}{=}{d}{(}{n}{-}1{)}{A}{=}1.{(}1,5{-}1{)}{.}\dfrac{5.{π}}180$
${=}0,0436{m}{=}4,36{c}{m}$
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Vật lý 11 bài 28: Lăng kính
Số câu hỏi: 38
Copyright © 2021 HOCTAP247
