Chọn phương án đúng. Một tia sáng tới vuông góc với mặt AB của một lăng kính có

* Hướng dẫn giải

Ta có hình vẽ: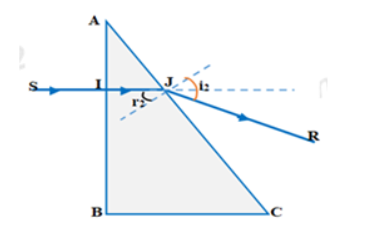


Tia tới: ${S}{I}{⊥}{A}{B}{⇒}{i}_1{=}0{⇒}{r}_1{=}0$
Góc tới mặt AC: ${r}_2{=}{∠A}{=}30^0$
Áp dụng định luật khúc xạ ánh sáng ta có:
${n}{.}{sin}{r}_2{=}{sin}{i}_2{⇒}{sin}{i}_2{=}{\sqrt{2}}{.}{sin}30{=}\dfrac{\sqrt{2}}2{⇒}{i}_2{=}45^0$

Góc lệch của tia sáng qua lăng kính là:
${D}{=}{i}_1{+}{i}_2{-}{A}{=}0{+}45^0{-}30^0{=}15^0$