Lăng kính thủy tinh có tiết diện thẳng là tam giác cân ABC đỉnh A. Một tia đơn

* Hướng dẫn giải

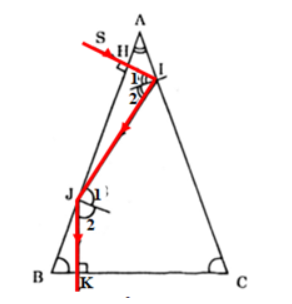
+ Ta có: SI⊥AB⇒Tia SI truyền thẳng vào môi trường trong suốt ABC mà không bị khúc xạ.
+ Góc tới mặt AC là: $∠I_1=∠I_2=A$
+ Mặt khác SI song song với pháp tuyến tại J ⇒$∠J_1=∠J_2=∠SIJ=2.I_1=2.∠A$
+ Vì JK⊥BC⇒$∠B=∠J_2=∠J_1=2.∠A$
+ Tam giác ABC cân tại $A ⇒∠B=∠C=2.∠A$
+ Tổng 3 góc trong tam giác ACB bằng:
$∠A+∠B + ∠C=180^0⇔∠A+2.∠A+2.∠A=180^0⇒∠A=36^0$