Vật AB = 10cm là một đoạn thẳng song song với trục chính của một thấu kính hội

* Hướng dẫn giải

Ta có hình sau: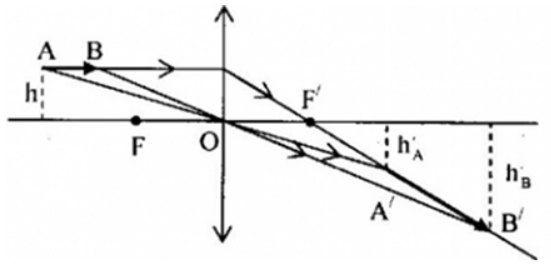

+ Ảnh A'B' nằm dọc tia ló ứng với tia truyền dọc theo AB
+ ${d}_{A}{=}30{+}10{=}40 cm{d}_{B}{=}30 cm$
Áp dụng công thức thấu kính: $\dfrac{1}{f}{=}\dfrac{1}{d}{+}\dfrac{1}{d'}$
+ Ta suy ra: $\left\{\begin{array}{l}
d_{A}^{\prime}=\frac{d_{A} f}{d_{A}-f}=\frac{40.20}{40-20}=40 \mathrm{~cm} \\
d_{B}^{\prime}=\frac{d_{B} f}{d_{B}-f}=\frac{30.20}{30-20}=60 \mathrm{~cm}
\end{array}\right.$
Và:
$\left\{\begin{array}{c}
\frac{h_{A}}{h}=\left|-\frac{d_{A}}{d_{A}}\right|=\frac{40}{40}=1 \rightarrow h_{A}=h=3 \mathrm{~cm} \\
\frac{h_{B}}{h}=\left|-\frac{d_{B}}{d_{B}}\right|=\frac{60}{20}=2 \rightarrow h_{B}=2 h=6 \mathrm{~cm}
\end{array}\right.$
Ảnh A'B' là ảnh thật, nghiêng góc với trục chính:
Độ lớn của ảnh:
${A}^{'}{B}^{'}{=}{\sqrt{\left({{d}_{B}^{'}{-}{d}_{A}^{'}}\right)^2{+}\left({{h}_{B}{-}{h}_{A}}\right)^2}}{=}{\sqrt{\left({60{-}40}\right)^2{+}\left({6{-}3}\right)^2}}{=}20,2 cm$