Cho ∆DEF vuông tại D. Gọi M, N, P lần lượt là trung điểm của DE, DF, EF.a) Chứng minh tứ giác MNFE là hình thang.b) Chứng minh tứ giác DMPN là hình chữ nhật.

* Hướng dẫn giải

Hướng dẫn giải

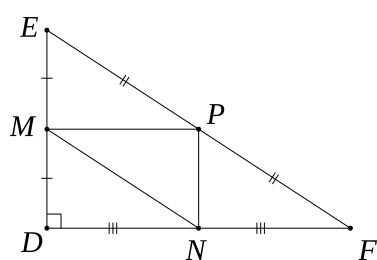
a) Xét tam giác DEF có:

M là trung điểm của DE

N là trung điểm của DF

⇒ MN là đường trung bình của tam giác DEF.

⇒ MN//EF, \(MN = \frac{1}{2}EF\)

⇒ MNFE là hình thang.

b) Xét tam giác DEF có:

M là trung điểm của DE

P là trung điểm của EF

⇒ MP là đường trung bình ΔDEF

⇒ MP//DF, \[MP = \frac{1}{2}DF\]

Lại có: N là trung điểm của DF

\[ \Rightarrow MP = DN = NF = \frac{1}{2}DF\]

Xét tứ giác DMPN có

MP = DN và MP//DN

⇒ DMPN là hình bình hành

Lại có: \[\widehat {EDF} = 90^\circ \]

⇒ DMPN là hình chữ nhật.