Cho ∆ABC có E là trung điểm của AC. Qua E kẻ ED//AB (D ∈ BC); EF//BC (F ∈ AB)a) Chứng minh tứ giác BDEF là hình bình hành và D là trung điểm của đoạn thẳng BC.b) Gọi H là điểm đối...

* Hướng dẫn giải

Hướng dẫn giải

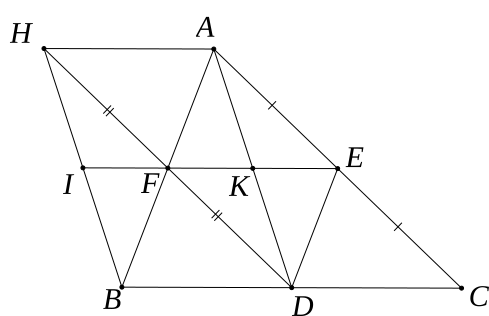
a)

EF // BD (vì EF//BC)

ED // FB (vì ED//AB)

Do đó tứ giác BDEF là hình bình hành (tứ giác có cặp cạnh đối song song)

Tam giác ABC có:

EA = EC (gt)

ED // AB (gt)

Do đó DB = DC hay D là trung điểm của đoạn thẳng BC.

b) Vì H đối xứng D qua F

⇒ F là trung điểm của HD (1)

Vì E là trung điểm của AC và EF//BC

⇒ F là trung điểm của AB (2)

Từ (1) và (2) ⇒ tứ giác HABD có hai đường chéo cắt nhau tại trung điểm mỗi đường.

⇒ AHBD là hình hình hành

⇒ HB//AD.

c) Xét tam giác HBD có:

I là trung điểm của HB

F trung điểm của HD

⇒ IF// BD (3)

Mà FE//BD (4)

⇒ I, F, E thẳng hàng.

⇒ I, K, E thẳng hàng.

d) Để \(HF = \frac{{AB}}{2}\) thì \(\frac{{HD}}{2} = \frac{{AB}}{2}\)

⇒ HD = AB

Hình bình hành AHBD có HD = AB

⇒ AHBD là hình chữ nhật

⇒ AD vuông góc với BC

Xét tam giác ABC có AD vừa là đường cao vừa là đường trung tuyến (D là trung điểm của BC)

⇒ ΔABC cân tại A.

Vậy ∆ABC cân tại A thì \(HF = \frac{{AB}}{2}\)