Cho hình bình hành ABCD (AD < AB), O là giao điểm hai đường chéo AC, BD. Gọi E, F lần lượt là hình chiếu của A và C trên BD.a) Chứng minh tứ giác AECF là hình bình hành.b) Gọi I là...

* Hướng dẫn giải

Hướng dẫn giải

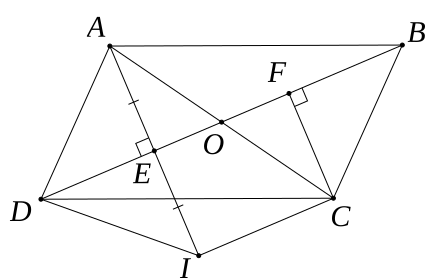
a) Hình bình hành ABCD có O là giao điểm của AC và BD

⇒ O là trung điểm của AC và BD.

⇒ OA = AC và OB = OD

Xét ΔOEA và ΔOFC có:

OA = OC

$\widehat{\mathrm{AOE}}=\widehat{\mathrm{COF}}$ (đối đỉnh)

$\widehat{\mathrm{AEO}}=\widehat{\mathrm{CFO}}=90°$

⇒ ΔOEA = ΔOFC (cạnh huyền – góc nhọn)

⇒ OE = OF

Xét tứ giác AECF có

OE = OF (cmt)

OA = OC (cmt)

⇒ AECF là hình bình hành (hai đường chéo cắt nhau tại trung điểm của mỗi đường)

b) I là điểm đối xứng của A qua BD

⇒ E là trung điểm của AI ⇒ AE = EI

Tam giác AIC có:

O là trung điểm của AC (cmt)

E là trung điểm của AI (cmt)

⇒ OE là đường trung bình tam giác AIC (đpcm)

⇒ OE // IC

c) Xét ΔAID có DE là đường trung trực của AI

⇒ ΔAID cân tại D

⇒ DE cũng là đường phân giác của góc ADI

$\Rightarrow \widehat{\mathrm{ADE}}=\widehat{\mathrm{IDE}}$

mà $\widehat{\mathrm{ADE}}=\widehat{\mathrm{CBF}}$(vì AD//BC)

$\Rightarrow \widehat{\mathrm{IDE}}=\widehat{\mathrm{CBF}}$

Tứ giác CIDB có:

BD // IC (vì OE // IC)

⇒ Tứ giác CIBD là hình than

Mà có $\widehat{\mathrm{IDE}}=\widehat{\mathrm{CBF}}$ (cmt)

⇒ CIBD là hình thang cân. (đpcm)