Cho hình bình hành ABCD. Gọi M là trung điểm của AB. Từ A kẻ đường thẳng song song với MC cắt DC tại N.a) Chứng minh: Tứ giác AMCN là hình bình hành.b) Trên thì BC lấy điểm I sao c...

* Hướng dẫn giải

Hướng dẫn giải

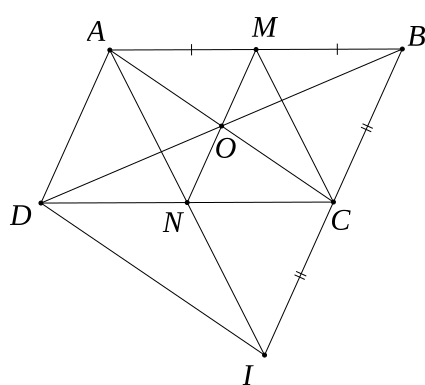
a) Ta có ABCD là hình bình hành (gt)

⇒ AB // CD; AB = CD; AD // BC; AD = BC

Mà M thuộc AB, N thuộc DC ⇒ AM // NC

Xét tứ giác AMCN có:

AM // NC (chứng minh trên)

AN // MC (giả thiết)

⇒ Tứ giác AMCN là hình bình hành.

b) AD // BC; I thuộc BC

⇒ AD // CI

Vì AD = BC (cmt); CI = BC (gt)

⇒ AD = CI

Xét tứ giác ACID có:

AD // CI (cmt)

AD = CI (cmt)

⇒ tứ giác ACID là hình bình hành

⇒ AC = DI.

c) AMCN là hình bình hành

⇒ AM = NC; O là trung điểm của AC

mà \[AM = \frac{1}{2}AB\] (M là trung điểm AB); AB = CD (cmt)

\[ \Rightarrow NC = \frac{1}{2}CD\]

⇒ N là trung điểm của CD

Xét ΔACD có:

O là trung điểm của AC (cmt)

N là trung điểm của CD (cmt)

⇒ NO là đường trung bình của ΔACD.

d) Tứ giác ACID có:

AC = DI

AD // CI

⇒ ACID là hình bình hành

Có N là trung điểm của CD

⇒ N là trung điểm AI

⇒ AN = NI, I thuộc AN

Ta có: MC // AN (AMCN là hình bình hành); I thuộc AN

⇒ MC // NI.