Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Đề kiểm tra Giữa kì 1 Toán 8 có đáp án (Mới nhất) !!
Cho hình thang vuông ABCD (∠A = ∠D = 90o)...
Cho hình thang vuông ABCD (∠A = ∠D = 90o) và CD = 2AB. Kẻ DH vuông góc với AC (H ∈ AC). Gọi M là trung điểm của HC, N là trung điểm của DH. Chứng minh rằng:
Câu hỏi :
Cho hình thang vuông ABCD (∠A = ∠D = 90o) và CD = 2AB. Kẻ DH vuông góc với AC (H ∈ AC). Gọi M là trung điểm của HC, N là trung điểm của DH. Chứng minh rằng:
a. MN ⊥ AD
b. ABMN là hình bình hành.
c. ∠BMD = 90o
Cho hình thang vuông ABCD (∠A = ∠D = 90o) và CD = 2AB. Kẻ DH vuông góc với AC (H ∈ AC). Gọi M là trung điểm của HC, N là trung điểm của DH. Chứng minh rằng:
a. MN ⊥ AD
b. ABMN là hình bình hành.
c. ∠BMD = 90o
* Đáp án
* Hướng dẫn giải

a. Vì ABCD là hình thang vuông nên ∠A = ∠D = 90o
⇒ AD ⊥ DC tại D (1)
Xét tam giác HDC ta có:
NH = ND (giả thiết)
MH = Mc (giả thiết)
⇒ NM là đường trung bình của tam giác HDC
⇒ NM // DC (2)
Từ (1) và (2) suy ra MN ⊥ AD tại G (từ vuông góc đến song song)

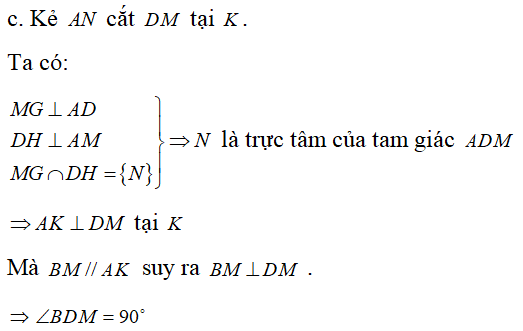
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra Giữa kì 1 Toán 8 có đáp án (Mới nhất) !!
Số câu hỏi: 24
Copyright © 2021 HOCTAP247
