Cho ABC vuông tại A (AB < AC). Gọi I là trung điểm BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N. a. Tứ giác AMIN là hình gì? Vì sao? b. Gọi D là điểm đối xứn...
Câu hỏi :
Cho ABC vuông tại A (AB < AC). Gọi I là trung điểm BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.
a. Tứ giác AMIN là hình gì? Vì sao?
b. Gọi D là điểm đối xứng của I qua N. Chứng minh ADCI là hình thoi.
c. Đường thẳng BN cắt DC tại K. Chứng minh
* Đáp án
* Hướng dẫn giải
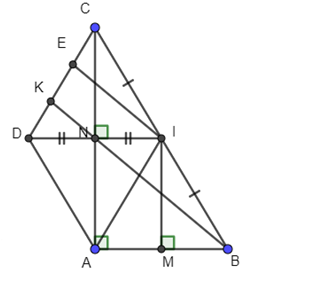
a. Chứng minh đúng ANIM là hình chữ nhật có 3 góc vuông:
Xét tứ giác ANIM có:
b. - Giải thích được IN vừa là đường cao vừa là trung tuyến của tam giác AIC:
Xét , có: AI = (tính chất đường trung tuyến trong tam giác vuông ABC)
cân tại I
Mà hay IN là đường cao
IN là đường trung tuyến
N là trung điểm của AC.
- Chứng minh ADCI là hình bình hành có hai đường chéo vuông góc:
Xét tứ giác ADCI, có:
Hai đường chéo AC và AI cắt nhau tại N.
Mà N là trung điểm của AC, N là trung điểm của DI.
Suy ra tứ giác ADCI là hình bình hành.
Mặt khác tại N
Do đó tứ giác ADCI là hình thoi.c. - Kẻ thêm đường thẳng qua I song song với BK cắt CD tại E và chứng minh được EK = EC:
Kẻ đường thẳng qua I song song với BK cắt CD tại E.
Xét , có:
I là trung điểm của BC (gt)
IE // BK
Suy ra E là trung điểm của KC hay EC = EK (1).
- Chứng minh được EK = DK:
Xét , có:
N là trung điểm của DI (gt)
NK // IE (BK // IE)
Suy ra K là trung điểm của DE hay DK = KE (2)
- Từ (1) và (2) Suy raCâu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề kiểm tra Học kì 1 Toán 8 có đáp án (Mới nhất) !!
Copyright © 2021 HOCTAP247
