Trang chủ Đề thi & kiểm tra Lớp 8 Toán học Bộ đề kiểm tra Học kì 1 Toán 8 có đáp án (Mới nhất) !! Cho tam giác ABC vuông tại A có AH là...

Cho tam giác ABC vuông tại A có AH là đường cao. Từ H vẽ HD vuông góc với cạnh AB tại D, vẽ HE vuông góc với cạnh AC tại E. Biết AB = 15cm, BC = 25 cm. a) Tính độ dài cạnh AC và di...

Toán học - Lớp 8

Trắc nghiệm Toán 8 Bài 1 Liên hệ giữa thứ tự và phép cộng

Trắc nghiệm Bài 2 Liên hệ giữa thứ tự và phép nhân - Luyện tập - Toán 8

Trắc nghiệm Toán 8 Bài 1 Nhân đơn thức với đa thức

Trắc nghiệm Hình học 8 Bài 1 Tứ giác

Trắc nghiệm Toán 8 Bài 2 Nhân đa thức với đa thức

Trắc nghiệm Toán 8 Bài 3 Những hằng đẳng thức đáng nhớ

Trắc nghiệm Toán 8 Bài 4 Những hằng đẳng thức đáng nhớ (tiếp)

Trắc nghiệm Toán 8 Bài 5 Những hằng đẳng thức đáng nhớ (tiếp)

Trắc nghiệm Toán 8 Bài 6 Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung

Trắc nghiệm Toán 8 Bài 7 Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức

Trắc nghiệm Toán 8 Bài 8 Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử

Trắc nghiệm Toán 8 Bài 9 Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp

Trắc nghiệm Toán 8 Bài 10 Chia đơn thức cho đơn thức

Trắc nghiệm Toán 8 Bài 11 Chia đa thức cho đơn thức

Đề thi học kì 2 môn Toán Lớp 8 - Trường THCS Phạm Công Bình năm học 2019

Trắc nghiệm Toán 8 Bài 12 Chia đa thức một biến đã sắp xếp

Trắc nghiệm Hình học 8 Bài 2 Hình thang

Trắc nghiệm Hình học 8 Bài 3 Hình thang cân

Trắc nghiệm Hình học 8 Bài 4 Đường trung bình của tam giác, của hình thang

Trắc nghiệm Hình học 8 Bài 6 Đối xứng trục

Trắc nghiệm Hình học 8 Bài 7 Hình bình hành

Trắc nghiệm Hình học 8 Bài 8 Đối xứng tâm

Trắc nghiệm Hình học 8 Bài 9 Hình chữ nhật

Trắc nghiệm Hình học 8 Bài 11 Hình thoi

Trắc nghiệm Hình học 8 Bài 12 Hình vuông

Câu hỏi :

Cho tam giác ABC vuông tại A có AH là đường cao. Từ H vẽ HD vuông góc với cạnh AB tại D, vẽ HE vuông góc với cạnh AC tại E. Biết AB = 15cm, BC = 25 cm.

a) Tính độ dài cạnh AC và diện tích tam giác ABC

b) Chứng minh tứ giác ADHE là hình chữ nhật

c) Trên tia đối của tia AC lấy điểm F sao cho . Chứng minh tứ giác AFDH là hình bình hành

d) Gọi K là điểm đối xứng của B qua A, gọi M là trung điểm của AH. Chứng minh: CM vuông góc với HK

* Đáp án

* Hướng dẫn giải

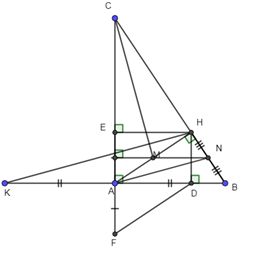
a) $Δ A B C$ vuông tại A

$\Rightarrow A B^{2} + A C^{2} = B C^{2}$ (định lý Py–ta–go)

$A C^{2} = B C^{2} - A B^{2} = 25^{2} - 15^{2}$

$= 625 - 225 = 400$

$\Rightarrow A C = \sqrt{400} = 20 (c m) (A C > 0)$

$S_{A B C} = \frac{1}{2} A B . A C = \frac{1}{2} .15.20$

= 150 (c m^{2})

b) Tứ giác ADHE có: $\hat{D A E} = 90 °$ (gt)

$\hat{A D H} = 90 ° (H D ⊥ A B)$

$\hat{A E H} = 90 ° (H E ⊥ A C)$

Do đó tứ giác ADHE là hình chữ nhật (dấu hiệu nhận biết).

c) Ta có $A F = A E$ (gt), AE=DH (tứ giác ADHE là hình chữ nhật) $\Rightarrow A F = D H$

Tứ giác AFDH có AF//DH, AF=DH

suy ra Tứ giác AFDH là hình bình hành (dấu hiệu nhận biết).

d) Gọi N là trung điểm của đoạn thẳng BH

Ta có M, N lần lượt là trung điểm của AH, BH

Suy ra MN là đường trung bình của tam giác HAB $\Rightarrow M N // A B$

Mà $A B ⊥ A C (\hat{A} = 90 °)$

Nên $M N ⊥ A C$

$Δ A C N$ có MN, AH là hai đường cao cắt nhau tại M

$\Rightarrow$ M là trực tâm của tam giác CAN

$\Rightarrow$ CM là đường cao của tam giác CAN $\Rightarrow A M ⊥ A N$

Mặt khác A, N lần lượt là trung điểm của BK, HB

$\Rightarrow$ AN là đường trung bình của tam giác BKH $\Rightarrow A N // H K$

Ta có $C M ⊥ A N$ , $A N // H K$

Vậy

C M ⊥ H K