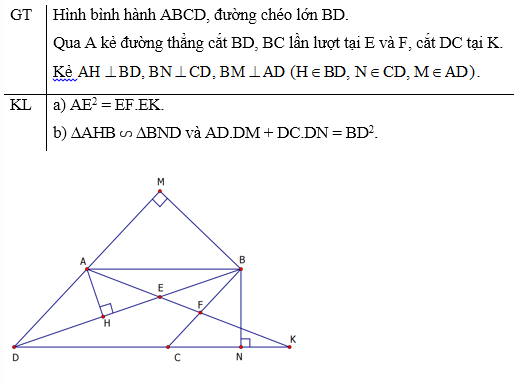
Cho hình bình hành ABCD, đường chéo lớn BD. Qua A kẻ đường thẳng cắt các đoạn thẳng BD, BC lần lượt tại E và F, cắt DC tại K. a) Chứng minh AE^2 = EF.EK. b) Kẻ AH vuông góc BD, BN...

Vì ABCD là hình bình hành nên:

+ AD // BC hay AD // BF

+ AB // CD hay AB // DK.

Áp dụng định lý Ta-let, ta có:

+ AD // BF suy ra: $\frac{AE}{EF}=\frac{ED}{EB}$  (1)

+ AB // DK suy ra: $\frac{ED}{EB}=\frac{EK}{AE}$ (2)

Từ (1) và (2) suy ra: $\frac{AE}{EF}=\frac{EK}{AE}$.

Do đó AE² = EF.EK (đpcm).

b) Xét ∆AHB và ∆BND có:

$\widehat{AHB}=\widehat{BND}={90}^o$

$\widehat{ABH}=\widehat{BDN}$ (AB // DK, hai góc so le trong)

Do đó ∆AHB  ∆BND (g.g) (đpcm)

Suy ra $\frac{AB}{BD}=\frac{BH}{DN}\frac{AB}{BD}=\frac{BH}{DN}$$\iff$ AB.DN = BD.BH

Mà AB = DC nên DC.DN = BD.BH (1)

Xét ∆ADH và ∆BDM có:

$\widehat{AHD}=\widehat{BMD}={90}^o$

$\widehat{BDM}$ chung.

Do đó ∆ADH ∆BDM (g.g).

Suy ra $\frac{AD}{DB}=\frac{DH}{DM}$ $\iff$AD.DM = DH.DB   (2)

Từ (1) và (2) suy ra: AD.DM + DC.DN = BD.BH + DH.DB = BD.(BH + HD)

= BD.BD = BD².

Do đó AD.DM + DC.DN = BD² (đpcm).