Cho hình thang ABCD (AB // CD). Gọi O là giao điểm của hai đường chéo AC và BD. Qua O kẻ đường thẳng song song với AB, cắt AD và BC theo thứ tự ở E và G. a) Chứng minh: OA . OD = O...

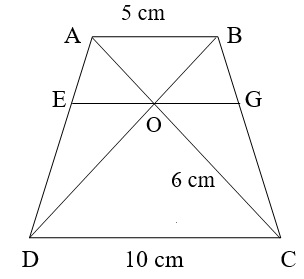
a) Ta có AB // CD, áp dụng định lý Ta-let: $\frac{OA}{OC}=\frac{OB}{OD}$.

Do đó: OA . OD = OB . OC (đpcm).

b) Từ câu a suy ra: $\frac{OA}{OC}=\frac{OB}{OD}=\frac{AB}{CD}$

$\iff \frac{OA}{6}=\frac{5}{10}=\frac{1}{2}$

$\iff OA=\frac{6}{2}=3$ (cm).

Do OE // DC nên theo hệ quả định lí Ta-let:

$\frac{AE}{AC}=\frac{AO}{AC}=\frac{EO}{DC}$

$\iff \frac{3}{3+6}=\frac{EO}{10}$

$\iff EO=\frac{3.10}{9}=\frac{10}{3}$ (cm).

Vậy OA = 3 cm, $EO=\frac{10}{3}$ cm.

c) Do OE // AB, theo hệ quả định lý Ta-lét ta có: $\frac{OE}{AB}=\frac{DE}{DA}$  (1)

Do OE // CD, theo hệ quả định lý Ta-lét ta có: $\frac{OE}{DC}=\frac{AE}{DA}$  (2)

Cộng vế theo vế của (1) và (2) ta được: $\frac{OE}{AB}+\frac{OE}{DC}=\frac{DE}{DA}+\frac{AE}{DA}=1$.

Suy ra $OE(\frac{1}{AB}+\frac{1}{CD})=1$ hay $\frac{1}{OE}=\frac{1}{AB}+\frac{1}{CD}$ (*)

Chứng minh tương tự, ta có: $\frac{1}{OG}=\frac{1}{AB}+\frac{1}{DC}$ (**)

Từ (*) và (**) suy ra: $\frac{1}{OE}=\frac{1}{OG}=\frac{1}{AB}+\frac{1}{CD}$ (đpcm).