Đề kiểm tra cuối kì 2 Toán 8 có đáp án ( Mới nhất) !!
Câu 1 :
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
A. 0x + 25 = 0
B.
Câu 2 :
Tập nghiệm của phương trình x2 – x = 0 là:
Tập nghiệm của phương trình x2 – x = 0 là:
A. S ={0}
B. S = {0; 1}
C. S = {1}
D. Một kết quả khác.
Câu 3 :
Bất đẳng thức nào sau đây là đúng?
Bất đẳng thức nào sau đây là đúng?
A. (−5) . 3 ≤ 16
B. (−5) + 3 ≥ 1
C. 15 + (−3) ≥ 18 + (−3)
Câu 4 :
Nếu ∆ABC đồng dạng với ∆A’B’C’ theo tỉ số k thì ∆A’B’C’ đồng dạng với ∆ABC theo tỉ số nào?
Nếu ∆ABC đồng dạng với ∆A’B’C’ theo tỉ số k thì ∆A’B’C’ đồng dạng với ∆ABC theo tỉ số nào?
A.
C.
D. 1.
Câu 5 :
Nếu a < b thì . Dấu thích hợp điền vào ô trống là:
Nếu a < b thì . Dấu thích hợp điền vào ô trống là:
A. ≥
B. ≤
C. <
D. >
Câu 6 :
Hình hộp chữ nhật có chiều dài bằng 5 cm, chiều rộng bằng 3 cm, chiều cao bằng 4 cm thì có thể tích là:
Hình hộp chữ nhật có chiều dài bằng 5 cm, chiều rộng bằng 3 cm, chiều cao bằng 4 cm thì có thể tích là:
A. 12 cm3
Câu 11 :
Hình hộp chữ nhật là hình có bao nhiêu mặt?
Hình hộp chữ nhật là hình có bao nhiêu mặt?
A. 6 đỉnh , 8 mặt , 12 cạnh;
B. 8 đỉnh , 6 mặt , 12 cạnh;
C. 12 đỉnh , 6 mặt , 8 cạnh;
D. 6 đỉnh , 12 mặt , 8 cạnh.
Câu 12 :
Điều kiện xác định của phương trình là:
Điều kiện xác định của phương trình là:
A. x ≠ 0 hoặc x ≠ 3;
B. x ≠ 0 hoặc x ≠ −3;
C. x ≠ 0 và x ≠ 3;
D. x ≠ 3.
Câu 13 :
Tập nghiệm của phương trình x(x + 1) = 0 là:
Tập nghiệm của phương trình x(x + 1) = 0 là:
A. S = {–1};
B. S = {0; –1};
C. S = {0};
D. S = {1; 0}.
Câu 14 :
Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
A. x + y > 8;
B. 0x + 5 ≥ 0;
C. x – 3 > 4 ;
D. (x – 7)2 ≤ 6x.
Câu 15 :
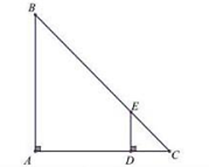
Hình sau biểu diễn tập nghiệm của bất phương trình nào?
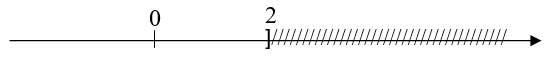
Hình sau biểu diễn tập nghiệm của bất phương trình nào?
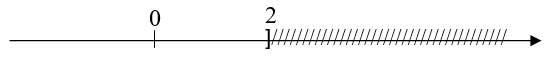
Câu 16 :
Trong các khẳng định sau, khẳng định nào không đúng?
Trong các khẳng định sau, khẳng định nào không đúng?
A. Hình hộp chữ nhật là hình lăng trụ đứng;
B. Các mặt bên của hình lăng trụ đứng là hình chữ nhật;
C. Các cạnh bên của hình lăng trụ đứng không bằng nhau;
D. Hình lăng trụ đứng có đáy là hình bình hành gọi là hình hộp đứng.
Câu 21 :
Tập nghiệm của phương trình là:
Tập nghiệm của phương trình là:
A. ;
B. ;
C. ;
D. .
Câu 22 :
Nghiệm của bất phương trình: 12 – 3x ≤ 0 là:
Nghiệm của bất phương trình: 12 – 3x ≤ 0 là:
B. x ≥ 4;
C. x ≤ − 4;
D. x ≥ − 4.
Câu 23 :
Cho tam giác ABC đồng dạng với tam giác MNP và .
Cho tam giác ABC đồng dạng với tam giác MNP và .
B. ;
C. ;
D. .
Câu 44 : Giải các phương trình sau
Câu 69 :
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) 3(x – 5) < x + 7;
b) .
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) 3(x – 5) < x + 7;
b) .
Câu 75 :
Giải các phương trình sau:
c)
Giải các phương trình sau:
c)
Câu 80 :
b) Chứng minh AH2 = HB.HC.
b) Chứng minh AH2 = HB.HC.
Câu 81 :
c) Trên tia HC, lấy H = HA. Từ D vẽ đường thẳng song song AH cắt AC tại E.
Chứng minh AE = AB.
c) Trên tia HC, lấy H = HA. Từ D vẽ đường thẳng song song AH cắt AC tại E.
Chứng minh AE = AB.
Câu 83 :
Giá trị x = - 4 là nghiệm của phương trình nào sau đây?
Giá trị x = - 4 là nghiệm của phương trình nào sau đây?
A. -2x = -8;
B. -2x = 8;
C. 2x - 8 = 0;
D. 3x - 1 = x + 7.
Câu 84 :
Phương trình x - 2 = 5 tương đương với phương trình
Phương trình x - 2 = 5 tương đương với phương trình
A. 2x = 14;
B. (x - 2)x = 5;
C. |x - 2| = 5;
D. (x - 2)2 = 25.
Câu 85 :
Cho a < b. Khẳng định nào sau đây đúng?
Cho a < b. Khẳng định nào sau đây đúng?
A. -2a < -2b;
B. -2a > -2b;
C. a - 1 > b - 1;
D. a + 2 > b + 2.
Câu 86 :
Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào?
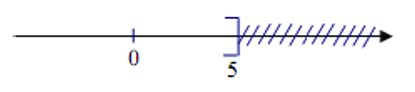
Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào?
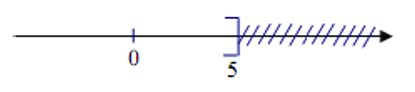
A. x ³ 5;
B. x > 5;
C. x £ 5;
D. x < 5.
Câu 87 :
Tập nghiệm của phương trình (x2 + 1)(x - 2) = 0 là
Tập nghiệm của phương trình (x2 + 1)(x - 2) = 0 là
A. S = {-1; -2};
B. S = {-1; 2};
C. S = {-1};
D. S = {2}.
Câu 88 :
Số nghiệm của phương trình |x + 1| + 1 = 0 là
Số nghiệm của phương trình |x + 1| + 1 = 0 là
A. 0;
B. 1;
C. 2;
D. 3.
Câu 89 :
Điều kiện xác định của phương trình là
Điều kiện xác định của phương trình là
A. x ¹ 1;
B. x ¹ ± 1;
C. x ¹ 0;
D. x ¹ -1.
Câu 90 :
An có 60 000 đồng, An mua bút hết 15 000 đồng, còn lại An mua vở với giá mỗi quyển vở là 6 000 đồng. Số quyển vở An có thể mua nhiều nhất là
An có 60 000 đồng, An mua bút hết 15 000 đồng, còn lại An mua vở với giá mỗi quyển vở là 6 000 đồng. Số quyển vở An có thể mua nhiều nhất là
A. 7 quyển;
B. 8 quyển;
C. 9 quyển;
Câu 91 :
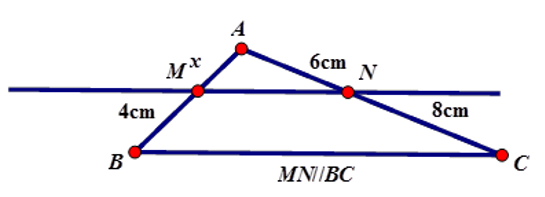
Cho DABC có MN // BC (với M Î AB; N Î AC). Khi đó
A.
B.
C.
D.
Câu 92 :
Cho ∆ABC ᔕ ∆MNP với tỉ số đồng dạng là . Khi đó tỉ số chu vi của DABC và DMNP là
Cho ∆ABC ᔕ ∆MNP với tỉ số đồng dạng là . Khi đó tỉ số chu vi của DABC và DMNP là
A.
B.
C.
D.
Câu 93 :
Cho DABC vuông tại A, có AB = 3cm, BC = 5cm. Tia phân giác của cắt BC tại E thì bằng
Cho DABC vuông tại A, có AB = 3cm, BC = 5cm. Tia phân giác của cắt BC tại E thì bằng
A.
B.
C.
D.
Câu 94 :
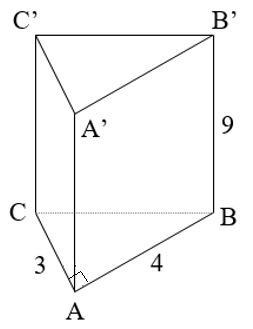
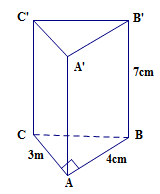
Hình hộp chữ nhật ABCD.A’B’C’D’ có AB = 3cm; BC = 5cm; AA’ = 4cm (hình vẽ). Khi đó thể tích của hình hộp chữ nhật là
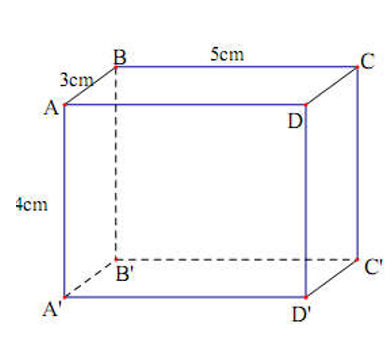
Hình hộp chữ nhật ABCD.A’B’C’D’ có AB = 3cm; BC = 5cm; AA’ = 4cm (hình vẽ). Khi đó thể tích của hình hộp chữ nhật là

A. 60 cm;
B. 60 cm2;
C. 60 cm3;
D. 6 dm3.
Câu 109 :
Giải các phương trình
d)
Giải các phương trình
d)
Câu 114 :
b) Chứng minh: HN.HI = HK.HP.
b) Chứng minh: HN.HI = HK.HP.
Câu 115 :
c) Chứng minh: NI.NH + PK.PH = NP2.
c) Chứng minh: NI.NH + PK.PH = NP2.
Câu 117 :
Giải các phương trình:
1) x - 9 = 0
Giải các phương trình:
1) x - 9 = 0
Câu 119 :
Giải các phương trình:
3)
Giải các phương trình:
3)
Câu 121 :
1) Cho m > n, chứng tỏ 2 + m > 2 + n.
1) Cho m > n, chứng tỏ 2 + m > 2 + n.
Câu 127 :
2) Chứng minh: AH2 = HB.HC.
2) Chứng minh: AH2 = HB.HC.
Câu 129 :
Giải các phương trình
b)
Giải các phương trình
b)
Câu 136 :
b) Chứng minh: AF.AB = AE.AC
b) Chứng minh: AF.AB = AE.AC
Câu 140 :
Giải các phương trình sau:
c)
Giải các phương trình sau:
c)
Câu 145 :
Cho ∆ABC nhọn (AB < AC) có đường cao BE, CF cắt nhau tại H.
a) Chứng minh: ∆FHB và ∆EHC đồng dạng.
Cho ∆ABC nhọn (AB < AC) có đường cao BE, CF cắt nhau tại H.
a) Chứng minh: ∆FHB và ∆EHC đồng dạng.
Câu 146 :
b) Chứng minh AF.AB = AE.AC..
b) Chứng minh AF.AB = AE.AC..
Câu 148 : Bất phương trình nào là bất phương trình bậc nhất một ẩn?
A.
B.
C. 2x2 + 3 > 0;
D. 2x + 1 - 2(x + 3) > 0.
Câu 149 :
Giá trị k sao cho phương trình 2x + k = x - 1 có nghiệm x0 = -2 là
Giá trị k sao cho phương trình 2x + k = x - 1 có nghiệm x0 = -2 là
A. k = -2;
B. k = -1;
C. k = 1;
D. k = 2.
Câu 150 :
Tập nghiệm của phương trình x2 - 3x = 0 là
Tập nghiệm của phương trình x2 - 3x = 0 là
A. S = {0};
B. S = {0; 3};
C. S = {3};
D. S = {0; -3}.
Câu 151 :
Điều kiện xác định của phương trình
Điều kiện xác định của phương trình
A. x ¹ -1; x ¹ 2;
B. x ¹ 0;
C. x ¹ 2; x ¹ ±1;
D. x ¹ 1; x ¹ 2.
Câu 152 :
Tập nghiệm của bất phương trình 5 - 2x ³ 0 là
Tập nghiệm của bất phương trình 5 - 2x ³ 0 là
A.
B.
C.
D.
Câu 153 :
Giá trị x = 2 là nghiệm của phương trình
Giá trị x = 2 là nghiệm của phương trình
A. 3x + 3 = 9;
B. -5x = 4x + 1;
C. x - 2x = -2x + 4;
D. x - 6 = 5 - x.
Câu 154 :
Phương trình |x - 3| = 9 có tập nghiệm là
Phương trình |x - 3| = 9 có tập nghiệm là
A. {-6; 12};
B. {6};
C. {12};
D. {-12}.
Câu 155 :
Nếu -2a > -2b thì
Nếu -2a > -2b thì
A. a < b;
B. a = b;
C. a > b;
D. a £ b.
Câu 156 :
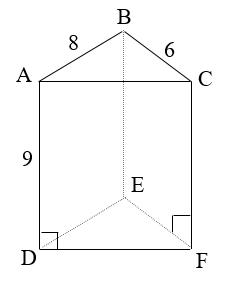
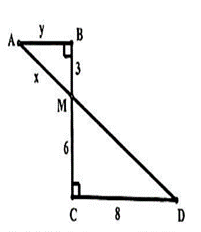
Cho hình vẽ, biết AB = BC = 5 cm, DC = 8 cm. Diện tích của tam giác HBC là
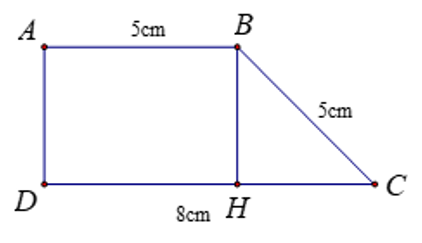
Cho hình vẽ, biết AB = BC = 5 cm, DC = 8 cm. Diện tích của tam giác HBC là

A. 4,5 cm2;
B. 6 cm2;
C. 12 cm2;
D. 16 cm2.
Câu 158 :
Cho tam giác ABC đồng dạng với tam giác MNP theo tỉ số 2. Khẳng định đúng là
Cho tam giác ABC đồng dạng với tam giác MNP theo tỉ số 2. Khẳng định đúng là
A. MN = 2.AB;
B. AC = 2.NP;
C. MP = 2.BC;
D. BC = 2.NP.
Câu 159 :
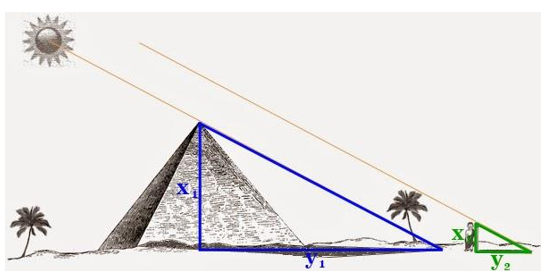
Hình dưới đây mô tả cách đo chiều cao của cây. Các thông số đo đạc được như sau: AB = 1 m; AA' = 4,5 m; CA = 1,2 m. Chiều cao của cây là
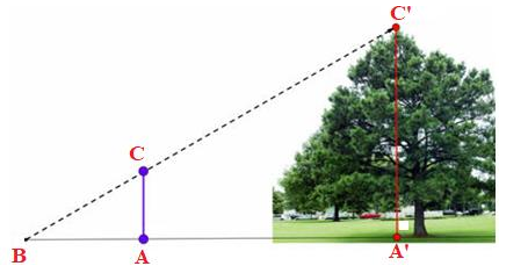
Hình dưới đây mô tả cách đo chiều cao của cây. Các thông số đo đạc được như sau: AB = 1 m; AA' = 4,5 m; CA = 1,2 m. Chiều cao của cây là

A. 5 (m);
B. 4,5 (m);
C. 6,6 (m);
D. 4 (m).
Câu 165 :
2. Chứng minh CI2 = IH.IB;
2. Chứng minh CI2 = IH.IB;
Câu 168 :
2. Tìm giá trị của x để |A| = A.
2. Tìm giá trị của x để |A| = A.
Câu 171 :
Giải các phương trình sau:
b.
Giải các phương trình sau:
b.
Câu 176 :
Lấy điểm M trên cạnh AC (M khác A và C), kẻ CI vuông góc với BM tại I. Chứng minh: MA.MC = MB.MI.
Lấy điểm M trên cạnh AC (M khác A và C), kẻ CI vuông góc với BM tại I. Chứng minh: MA.MC = MB.MI.
Câu 178 :
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
A. 0x - 1 = 0;
B. x2 + 2 = 0;
C. x + 0 = 0;
D. x + y = 0.
Câu 179 :
Giá trị x = 2 là nghiệm của phương trình nào sau đây?
Giá trị x = 2 là nghiệm của phương trình nào sau đây?
A. x + 2 = 0;
B. 2x - 2 = 0;
C. 2x + 2 = 0;
D. x - 2 = 0.
Câu 180 :
Tập hợp nghiệm của phương trình (x + 3)(x - 1) = 0 là
Tập hợp nghiệm của phương trình (x + 3)(x - 1) = 0 là
A. S = {1};
B. S = {-3};
C. S = {1; -3};
D. S = {-1; 3}.
Câu 181 :
Điều kiện xác định của phương trình là
Điều kiện xác định của phương trình là
A. x ¹ 2;
B. x ¹ -2;
C. x ¹ 2 và x ¹ 1;
D. x ¹ 2 và x ¹ 0.
Câu 182 :
Bất phương trình x - 1 £ 0 tương đương với bất phương trình nào sau đây?
Bất phương trình x - 1 £ 0 tương đương với bất phương trình nào sau đây?
A. x £ 0;
B. x £ 1;
C. x ³ 0;
D. x £ -1.
Câu 183 :
Tập nghiệm của bất phương trình 2x < 2 là
Tập nghiệm của bất phương trình 2x < 2 là
A. {x | x < 1};
B. {x | x < -1};
C. {x | x > 2};
D. {x | x < 2}.
Câu 184 :
Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào?
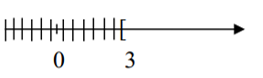
Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào?
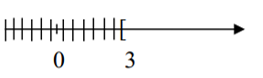
A. x £ 3;
B. x ³ 3;
C. x < 3;
D. x > 3.
Câu 185 :
Cho AB = 50 cm và CD = 10 dm; Tỉ số của hai đoạn thẳng AB và CD bằng
Cho AB = 50 cm và CD = 10 dm; Tỉ số của hai đoạn thẳng AB và CD bằng
A. 5;
B.
C. 2;
D.
Câu 186 :
Quan sát Hình 1, biết AD là đường phân giác của tam giác ABC. Tỉ số bằng tỉ số nào dưới đây?
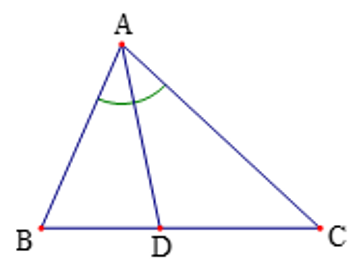
Quan sát Hình 1, biết AD là đường phân giác của tam giác ABC. Tỉ số bằng tỉ số nào dưới đây?

A.
B.
C.
D.
Câu 187 :
Cho ∆ABC, một đường thẳng a song song với BC cắt các cạnh AB và AC lần lượt ở D và E. Biết , tỉ số bằng
Cho ∆ABC, một đường thẳng a song song với BC cắt các cạnh AB và AC lần lượt ở D và E. Biết , tỉ số bằng
A.
B.
C.
D.
Câu 188 :
Nếu ∆MNP đồng dạng với ∆ABC theo tỉ số thì tỉ số diện tích của tam giác MNP và diện tích tam giác ABC bằng
Nếu ∆MNP đồng dạng với ∆ABC theo tỉ số thì tỉ số diện tích của tam giác MNP và diện tích tam giác ABC bằng
A.
B.
C.
D.
Câu 189 :
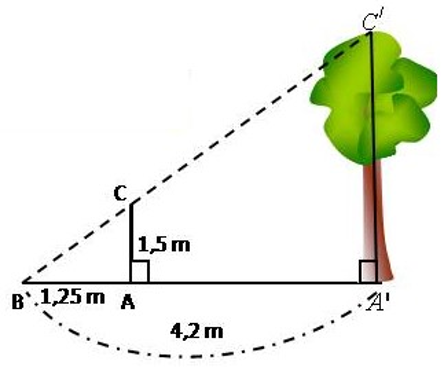
Bóng của một cây cột cờ trên mặt đất có độ dài 4,8m; cùng thời điểm đó một thanh sắt vuông góc với mặt đất cao 1m có bóng dài 0,4m. Vậy chiều cao của cây cột cờ là
Bóng của một cây cột cờ trên mặt đất có độ dài 4,8m; cùng thời điểm đó một thanh sắt vuông góc với mặt đất cao 1m có bóng dài 0,4m. Vậy chiều cao của cây cột cờ là
A. 10 m;
B. 11 m;
C. 12 m;
D. 13 m.
Câu 190 :
Cho biết hình hộp chữ nhật ABCD.A'B'C'D' có AB = 3cm, BC = 5cm, AA’ = 4cm.
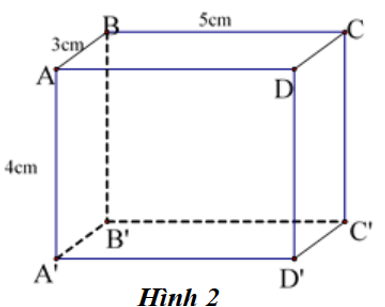
Đường thẳng C'D' song song với đường thẳng
Cho biết hình hộp chữ nhật ABCD.A'B'C'D' có AB = 3cm, BC = 5cm, AA’ = 4cm.

Đường thẳng C'D' song song với đường thẳng
A. A'B'.
B. BC.
C. AD.
D. AA'.
Câu 191 :
Diện tích xung quanh của hình hộp chữ nhật ABCD.A'B'C'D' là
Diện tích xung quanh của hình hộp chữ nhật ABCD.A'B'C'D' là
A. 15 cm2;
B. 20 cm2;
C. 32 cm2;
D. 64 cm2.
Câu 192 :
Thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là
Thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là
A. 15 cm3;
B. 20 cm3;
C. 32 cm3;
D. 60 cm3.
Câu 194 :
a) Giải các phương trình sau:
2)
a) Giải các phương trình sau:
2)
Câu 200 :
Phương trình 3x + 1 = -x + 9 có nghiệm là
Phương trình 3x + 1 = -x + 9 có nghiệm là
A. x = 2;
B. x = 5;
C. x = -2;
D. x = 3.
Câu 201 :
Nghiệm của bất phương trình 4 - 2x < 6 là
Nghiệm của bất phương trình 4 - 2x < 6 là
A. x > -5;
B. x < -5;
C. x < -1;
D. x > -1.
Câu 202 :
Hai biểu thức và có giá trị bằng nhau khi và chỉ khi
Hai biểu thức và có giá trị bằng nhau khi và chỉ khi
A.
B.
C.
D.
Câu 203 :
Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất một ẩn?
Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất một ẩn?
A. 2x + y > 0;
B. 2x2 - 6 < 0;
C. 2x + 5 ³ 0;
D. x(x + 1) > 0.
Câu 204 :
Số nghiệm của phương trình (1 - x)2 + 2x = x2 + 1 là
Số nghiệm của phương trình (1 - x)2 + 2x = x2 + 1 là
A. Một nghiệm;
B. Hai nghiệm;
C. Vô nghiệm;
D. Vô số nghiệm.
Câu 205 :
Tất cả các giá trị của k để phương trình 4x2 - 25 + k2 + 4kx = 0 có nghiệm x = -2 là
Tất cả các giá trị của k để phương trình 4x2 - 25 + k2 + 4kx = 0 có nghiệm x = -2 là
A. k = -1;
B. k = 9;
C. k = -1; k = 9;
D. k = 1; k = -9.
Câu 206 :
Cho đoạn thẳng AB = 2 dm và CD = 3 m, tỉ số của hai đoạn thẳng này là
Cho đoạn thẳng AB = 2 dm và CD = 3 m, tỉ số của hai đoạn thẳng này là
A.
B.
C.
D.
Câu 207 :
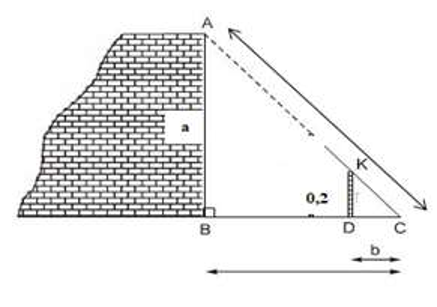
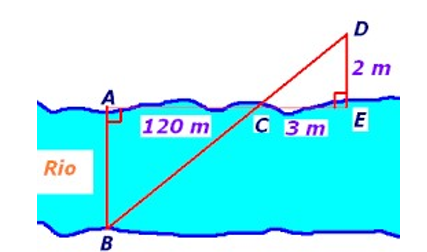
Một người thợ sử dụng thước ngắm có góc vuông để đo gián tiếp chiều cao của một cái cây. Với các kích thước đo được như hình bên: Khoảng cách từ vị trí gốc cây đến vị trí chân của người thợ là 2,25 m và từ vị trí chân đứng thẳng trên mặt đất đến mắt của người ngắm là 1,5 m. Hỏi với các kích thước trên thì người thợ đo được chiều cao của cây đó là bao nhiêu?
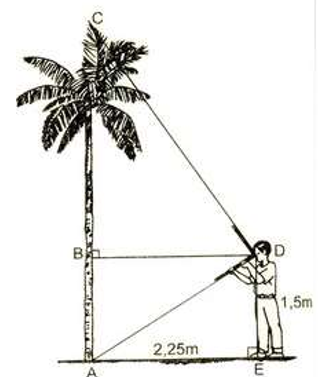
Một người thợ sử dụng thước ngắm có góc vuông để đo gián tiếp chiều cao của một cái cây. Với các kích thước đo được như hình bên: Khoảng cách từ vị trí gốc cây đến vị trí chân của người thợ là 2,25 m và từ vị trí chân đứng thẳng trên mặt đất đến mắt của người ngắm là 1,5 m. Hỏi với các kích thước trên thì người thợ đo được chiều cao của cây đó là bao nhiêu?

A. 3,25 m;
B. 4,875 m;
C. 5,625 m;
D. 4,5 m.
Câu 208 :
Cho ∆ABC vuông tại A có AB = 3cm, BC = 5cm, AD là đường phân giác trong của góc A (D thuộc BC). Tỉ số bằng
Cho ∆ABC vuông tại A có AB = 3cm, BC = 5cm, AD là đường phân giác trong của góc A (D thuộc BC). Tỉ số bằng
A.
B.
C.
D.
Câu 209 :
Hình hộp chữ nhật có:
Hình hộp chữ nhật có:
A. 6 đỉnh, 8 mặt, 12 cạnh;
B. 8 đỉnh, 6 mặt, 12 cạnh;
C. 12 đỉnh, 6 mặt, 8 cạnh;
D. 6 đỉnh, 12 mặt, 8 cạnh.
Câu 210 :
Nếu ∆ABC có MN // BC, (M Î AB, N Î AC) theo định lý Talet ta có:
Nếu ∆ABC có MN // BC, (M Î AB, N Î AC) theo định lý Talet ta có:
A.
B.
C.
D.
Câu 211 :
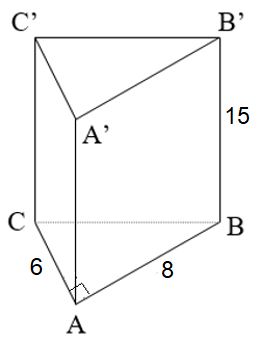
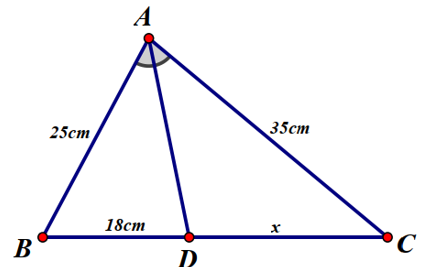
Cho tam giác ABC có AB = 9cm; AC = 12cm; BC = 15cm. Trên cạnh AB và AC lần lượt lấy hai điểm M và N sao cho AM = 3cm, AN = 4cm. Kết luận nào sau đây là sai?
Cho tam giác ABC có AB = 9cm; AC = 12cm; BC = 15cm. Trên cạnh AB và AC lần lượt lấy hai điểm M và N sao cho AM = 3cm, AN = 4cm. Kết luận nào sau đây là sai?
A. MN // BC;
B.
C.
D. DANM vuông.
Câu 216 :
Cho ∆ABC vuông tại A, đường cao AH.
a) Chứng minh ∆ABC đồng dạng với ∆HBA, từ đó suy ra AB2 = BH.BC.
Cho ∆ABC vuông tại A, đường cao AH.
a) Chứng minh ∆ABC đồng dạng với ∆HBA, từ đó suy ra AB2 = BH.BC.
Câu 220 :
Giải phương trình
a) 4x – 5 = 2x + 1
Giải phương trình
a) 4x – 5 = 2x + 1
Câu 222 :
Giải phương trình
c)
Giải phương trình
c)
Câu 228 :
b) Chứng minh: AK2 = KB.KC
b) Chứng minh: AK2 = KB.KC
Câu 232 :
Giải các phương trình sau:
c)
Giải các phương trình sau:
c)
Câu 234 :
Giải bất phương trình:
7x - 5 > 2x + 6
Giải bất phương trình:
7x - 5 > 2x + 6
Câu 239 :
b) Chứng minh: DADF đồng dạng với DABC.
b) Chứng minh: DADF đồng dạng với DABC.
Câu 240 :
c) Chứng minh: BH.BD + CH.CF = BC2 và
c) Chứng minh: BH.BD + CH.CF = BC2 và
Câu 242 :
Giải phương trình
b)
Giải phương trình
b)
Câu 244 :
Giải phương trình
d)
Giải phương trình
d)
Câu 251 :
Bất phương trình 2x - 3 > 5 có tập nghiệm biểu diễn bởi hình vẽ nào?
A.
B.
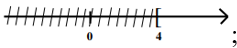
C.

D.

Câu 252 :
Trong các bất phương trình sau, đâu là bất phương trình bậc nhất một ẩn ?
Trong các bất phương trình sau, đâu là bất phương trình bậc nhất một ẩn ?
A. 2x - y > 0;
B. -3x - 2 £ 0;
C. x(x + 2) < 0;
D. 0x + 2 > 0.
Câu 253 :
Nếu một hình lập phương có cạnh là 5 cm thì thể tích của hình lập phương đó là
Nếu một hình lập phương có cạnh là 5 cm thì thể tích của hình lập phương đó là
A. 125 lít;
B. 25 cm3;
C. 25 cm2;
D. 125 cm3.
Câu 255 :
Cho ∆ABC ᔕ ∆DEF, biết AB = 3 cm; DE = 2 cm và diện tích của ∆DEF bằng 6 cm2. Diện tích của ∆ABC bằng:
A. 9 cm2;
B. 12 cm2;
C. 13,5 cm2;
D. 15,5 cm2.
Câu 263 :
c) Chứng minh rằng:
c) Chứng minh rằng:
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAP247