Cho hình bình hành ABCD và điểm F trên cạnh BC. Tia AF cắt BD và DC lần lượt ở E và G. Chứng minh: a) Chứng minh: ∆DEA ∆BEF và ∆DGE ∆BAE. b) Chứng minh: AE2 = EF . EG. c) Chứng min...
Câu hỏi :
Cho hình bình hành ABCD và điểm F trên cạnh BC. Tia AF cắt BD và DC lần lượt ở E và G. Chứng minh:
a) Chứng minh: ∆DEA 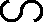 ∆BEF và ∆DGE
∆BEF và ∆DGE 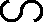 ∆BAE.
∆BAE.
b) Chứng minh: AE2 = EF . EG.
c) Chứng minh rằng BF. DG không đổi khi điểm F thay đổi trên BC.
Cho hình bình hành ABCD và điểm F trên cạnh BC. Tia AF cắt BD và DC lần lượt ở E và G. Chứng minh:
a) Chứng minh: ∆DEA ![]() ∆BEF và ∆DGE
∆BEF và ∆DGE ![]() ∆BAE.
∆BAE.
b) Chứng minh: AE2 = EF . EG.
c) Chứng minh rằng BF. DG không đổi khi điểm F thay đổi trên BC.
* Đáp án
* Hướng dẫn giải

Ta có ABCD là hình bình hành nên:
+ AD // BC hay BF // AD.
Khi đó: ; (các cặp góc so le trong).
+ AB // CD hay AB//GD.
(hai góc so le trong).
Xét ∆DEA và ∆BEF có:
(cmt).
(cmt).
Do đó ∆DEA ![]() ∆BEF (g.g).
∆BEF (g.g).
Xét ∆DGE và ∆BAE có:
(cmt)
(hai góc đối đỉnh)
Do đó ∆DGE ![]() ∆BAE (g.g).
∆BAE (g.g).
Vậy ∆DEA ![]() ∆BEF và ∆DGE
∆BEF và ∆DGE ![]() ∆BAE.
∆BAE.
b) Theo câu a, ta có:
+ ∆DEA ![]() ∆BEF suy ra: (1)
∆BEF suy ra: (1)
+ ∆DGE ![]() ∆BAE suy ra: (2)
∆BAE suy ra: (2)
Từ (1) và (2) suy ra .
Do đó: EA2 = EF . FG (đpcm).
c) Theo câu a, ta có:
+ ∆DEA ![]() ∆BEF suy ra: (3)
∆BEF suy ra: (3)
+ ∆DGE ![]() ∆BAE suy ra: (4)
∆BAE suy ra: (4)
Từ (3) và (4) suy ra .
Do đó: BF . DG = AD . AB (không đổi).
Vậy BF . DG không đổi khi F thay đổi trên BC.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra cuối kì 2 Toán 8 có đáp án ( Mới nhất) !!
Copyright © 2021 HOCTAP247
