Cho ABC vuông tại A, đường cao AH. a)Chứng minh ABC đồng dạng HBA và AB. AH = BH. AC.

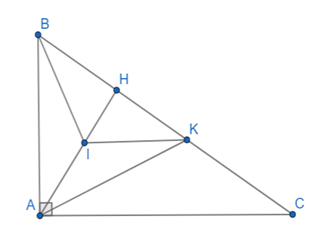
a) Vì DABC vuông tại A nên $\widehat{BAC}={90}^o$.

Mà AH là đường cao DABC hay AH ^ BC nên $\widehat{AHB}={90}^o$.

Do đó $\widehat{BAC}$ = $\widehat{AHB}$.

Xét DABC và DHBA có:

$\widehat{BAC}$ = $\widehat{AHB}$(cmt)

$\widehat{B}$ là góc chung.

Do đó DABC $\backsim$ DHBA (g.g)

Suy ra $\frac{AB}{HB}$ = $\frac{AC}{AH}$

Vậy AB. AH = AC. HB (đpcm)

b) Xét DAHB vuông tại H, ta có:

AB² = AH² + HB² (định lý Py-ta-go)

=> AH² = AB² − HB² = 25 − 9 = 16

=> AH = 4 (cm).

Vì BI là tia phân giác của $\widehat{ABC}$

=> $\frac{IA}{IH}$ = $\frac{AB}{BH}$ (tính chất đường phân giác trong tam giác)

=> $\frac{AH-HI}{IH}$= $\frac{AB}{BH}$ = $\frac{5}{3}$

<=> $\frac{AH}{IH}$− 1 = $\frac{5}{3}$

<=> $\frac{4}{IH}=\frac{8}{3}$

=> IH = $\frac{12}{8}$ = 1,5 (cm)

Ta có: AI = AH − IH = 4 − 1,5 = 2,5 (cm)

Vậy AI = 2,5 cm; HI = 1,5 cm.

c) Xét DABH và DCAH có:

$\widehat{AHB}=\widehat{AHC}={90}^o$

$\widehat{ABH}=\widehat{CAH}$ (cùng phụ $\widehat{BAH}$)

Do đó DABH  DCAH (g.g)

Suy ra $\frac{AH}{BH}=\frac{HC}{AH}$.

Suy ra AH² = BH. HC

<=>16 = 3. HC

=> HC = $\frac{16}{3}$

=> BC = $\frac{16}{3}$ + 3 = $\frac{25}{3}$ (cm)

+ AC² = BC² − AB²

=> AC² = ${\left(\frac{25}{3}\right)}^2$− 5² = $\frac{400}{9}$

=> AC = $\frac{20}{3}$ (cm).

Xét DHAC có AK là tia phân giác của $\widehat{HAC}$ nên:

$\frac{KH}{KC}$ = $\frac{AH}{AC}$ = $\frac{3}{5}$

Mà $\frac{HI}{IA}$ = $\frac{1,5}{2,5}$ = $\frac{3}{5}$

Suy ra $\frac{HI}{IA}$ = $\frac{KH}{KC}$