Cho tam giác ABC có ba góc nhọn, các đường cao BD và CE cắt nhau ở H. a)Chứng minh tam giác ABD đồng dạng tam giác ACE

* Hướng dẫn giải

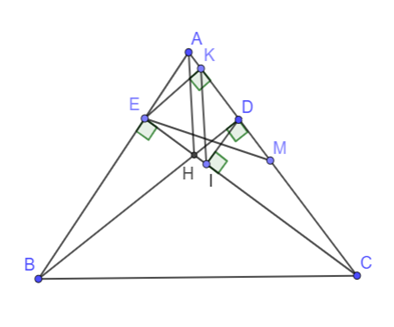
a) Vì BD và CE là đường cao của DABC nên BD ^ AC, CE ^ AB.

Suy ra $\widehat{ADB}={90}^o;\widehat{AEC}={90}^o$

Do đó $\widehat{ADB}=\widehat{AEC}$ .

Xét DABD và DACE có:

$\widehat{BAC}$ chung

$\widehat{ADB}=\widehat{AEC}$ (chứng minh trên)

Do đó DABD $\backsim$  DACE (g.g).

b) Xét DACE và DHCD có:

$\widehat{AEC}=\widehat{HDC}$ = 90° (vì BD ^ AC, CE ^ AB)

$\widehat{HCD}$ chung

Do đó D ACE $\backsim$  D HCD (g.g)

Suy ra $\frac{CA}{CH}=\frac{CE}{C\text{D}}$

Do đó CH. CE = CD. CA (đpcm).

c) Xét DCDI và DCEK có:

$\widehat{CID}=\widehat{CKE}$= 90° (vì EK ^ AC tại K; DI ^ EC tại I)

$\widehat{DCI}$ chung

Do đó D CDI $\backsim$  D CEK (g.g)

Suy ra  $\frac{CI}{CK}=\frac{CD}{CE}$

Theo câu b có: $\frac{CD}{CE}=\frac{CH}{CA}$ suy ra $\frac{CI}{CK}=\frac{CH}{CA}$

Khi đó $\frac{CI}{CH}=\frac{CK}{CA}$

Do đó KI // AH (theo định lý Ta-let đảo).