Cho tam giác ABC có AB = 5 cm; BC = 8 cm. Trên cạnh AB lấy điểm D sao cho AD = 2 cm.

Câu hỏi :

Cho tam giác ABC có AB = 5 cm; BC = 8 cm. Trên cạnh AB lấy điểm D sao cho AD = 2 cm. Qua D kẻ đường thẳng song song với BC cắt AC ở E và cắt đường thẳng qua C song song với AB ở F.

a) Tính DE.

b) BF cắt AC ở I. Tính $\frac{IF}{IB}$ .

c) Chứng minh rằng IC² = IE.IA.

d) BE cắt AF ở H. Tính $\frac{HA}{HF}$ .

* Đáp án

* Hướng dẫn giải

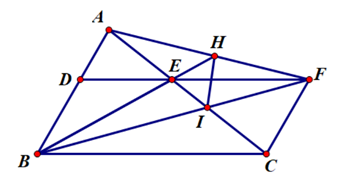
a)Áp dụng định lý Ta-let trong ∆ABC có DE // BC, ta có:

$\frac{AD}{AB}=\frac{DE}{BC}$

$\iff DE=\frac{AD.BC}{AB}=\frac{2.8}{5}=3,2$ (cm).

b) Theo đề ta có DE // BC hay DF // BC và BD // CF.

Suy ra tứ giác BDFC là hình bình hành nên ta có FC = BD.

Mà BD = AB – AD = 5 – 2 = 3 (cm).

Suy ra FC = 3 cm.

Ta có CF // AD (gt), áp dụng hệ quả của định lý Ta-let, ta có:

$\frac{IF}{IB}=\frac{FC}{AD}=\frac{3}{5}$

c) Áp dụng hệ quả của định lý Ta – let với CF // AD, ta có:

$\frac{IF}{IB}=\frac{IC}{IA}$ (1)

Áp dụng hệ quả định lý Ta – let với EF // BC, ta có:

$\frac{IF}{IB}=\frac{IE}{IC}$ (2)

Từ (1) và (2) suy ra $\frac{IC}{IA}=\frac{IE}{IC}=\frac{IF}{IB}$  nên IC² = IE.IA.