Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Bộ 14 đề thi Học kì 1 Toán 8 có đáp án !!
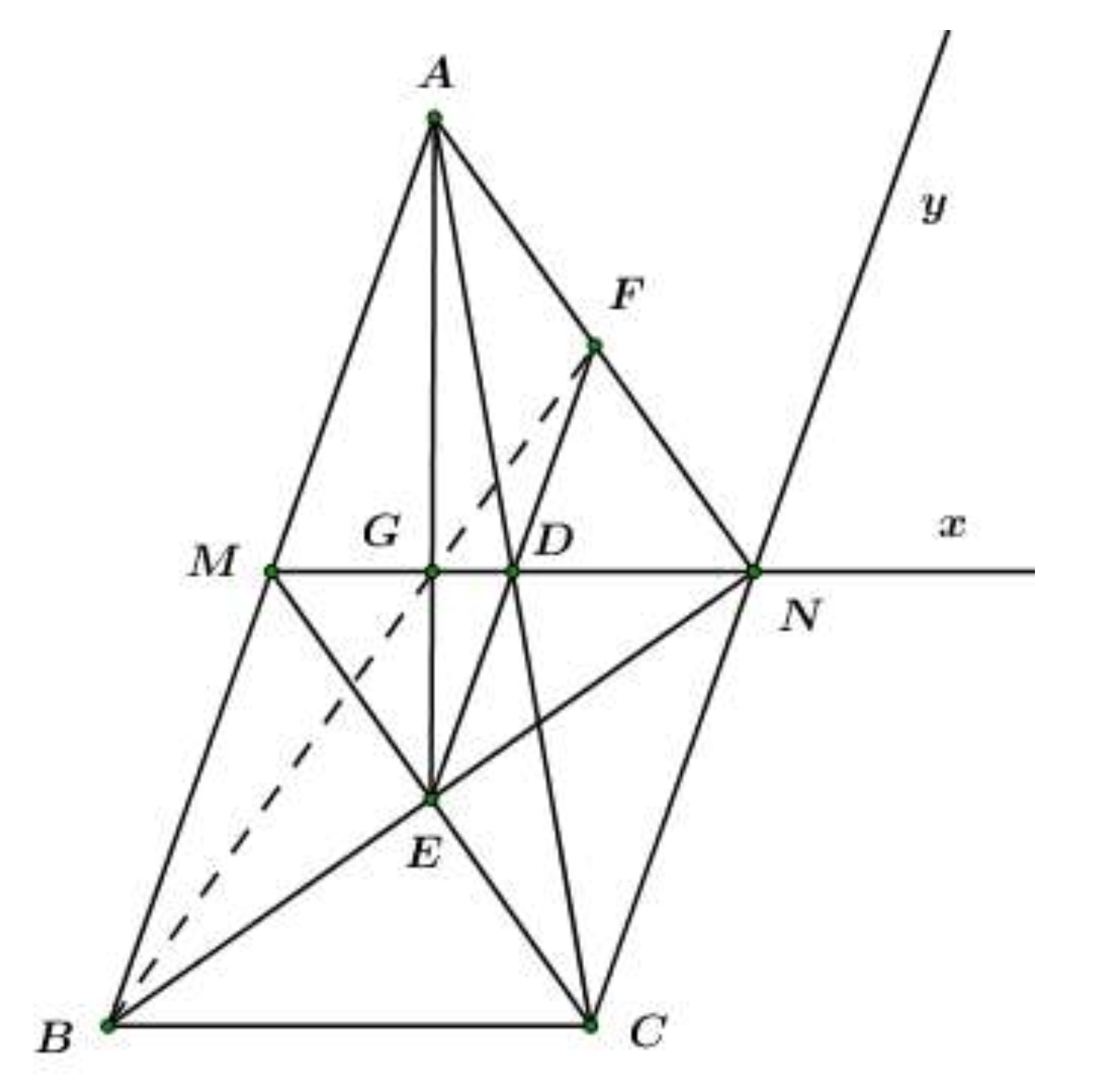
Gọi G là giao điểm của AE với MN. Chứng...
Gọi G là giao điểm của AE với MN. Chứng minh B, G, F thẳng hàng.
Câu hỏi :
Cho tam giác ABC có , từ trung điểm M của AB kẻ tia Mx song song BC, từ C kẻ tia Cy song song AB sao cho Mx cắt Cy tại N.
Gọi G là giao điểm của AE với MN. Chứng minh B, G, F thẳng hàng.
Cho tam giác ABC có , từ trung điểm M của AB kẻ tia Mx song song BC, từ C kẻ tia Cy song song AB sao cho Mx cắt Cy tại N.
Gọi G là giao điểm của AE với MN. Chứng minh B, G, F thẳng hàng.
* Đáp án
* Hướng dẫn giải
Phương pháp:
Sử dụng dấu hiệu nhận biết và tính chất của hình bình hành, dấu hiệu nhận biết tam giác vuông, chứng minh tam giác bằng nhau và tính chất trọng tâm của tam giác.
Cách giải:
Ta có: (cmt) .
Mà (AMCN là hình bình hành) và .
Vậy F là trung điểm AN.
Xét tam giác ABN có G là giao của hai đường trung tuyến AE và NM nên G là trọng tâm của tam giác ABN.
BG đi qua trung điểm F của AN B, G, F thẳng hàng.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ 14 đề thi Học kì 1 Toán 8 có đáp án !!
Số câu hỏi: 199
Copyright © 2021 HOCTAP247
