Kẻ $D E ⊥ A C$ , gọi K là trung điểm của EC. Qua K vẽ đường thẳng $d ⊥ D K$ . Chứng minh: Ba đường thẳng AH, MN và d đồng qui (cùng gặp nhau tại 1 điểm)

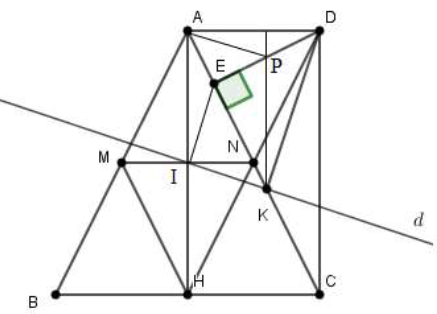
Media VietJack

Lấy P là trung điểm cạnh ED. Gọi I là giao điểm của MN và AH. Ta sẽ chứng minh $I K ⊥ D K$

Xét tam giác AHC có $I N // H C$ và N là trung điểm AC nên I là trung điểm của AH

Suy ra $A I = \frac{A H}{2}$ và $A I // D C$ ; $A H = D C$ (do ADCH là hình chữ nhật) nên $A I = \frac{D C}{2}$

Xét tam giác EPC có PK là đường trung bình của tam giác $\Rightarrow P K // D C$ , $P K = \frac{D C}{2}$

Xét tứ giác AIPK có $A I = P K (= \frac{D C}{2})$ ; $A I // P K // D C$ nên AIPK là hình bình hành.

Do đó: $I K // A P$

Lại có $P K // D C$ mà $D C ⊥ A D \Rightarrow P K ⊥ A D$

Từ đó suy ra P là trực tâm tam giác ADK.

Suy ra $A P ⊥ D K$ mà $I K // A P$ nên $I K ⊥ D K$

Do đó $I K \equiv d$ nên ba đường thẳng AH,MN, d đồng qui tại điểm I (đpcm).

Câu hỏi trên thuộc đề trắc nghiệm dưới đây !

Kẻ DE vuông góc với AC, gọi K là trung điểm của EC. Qua K vẽ đường thẳng d vuông góc

Câu hỏi :

Cho tam giác ABC cân tại A. Gọi M,N,H theo thứ tự là trung điểm của AB,AC và BC. Kẻ DE⊥AC , gọi K là trung điểm của EC. Qua K vẽ đường thẳng d⊥DK . Chứng minh: Ba đường thẳng AH, MN và d đồng qui (cùng gặp nhau tại 1 điểm)

* Đáp án

* Hướng dẫn giải

Bộ 14 đề thi Học kì 1 Toán 8 có đáp án !!

Cho tam giác ABC cân tại A. Gọi M,N,H theo thứ tự là trung điểm của AB,AC và BC.

Kẻ $D E ⊥ A C$ , gọi K là trung điểm của EC. Qua K vẽ đường thẳng $d ⊥ D K$ . Chứng minh: Ba đường thẳng AH, MN và d đồng qui (cùng gặp nhau tại 1 điểm)