Gọi M là trung điểm của BC. Tia AM cắt tia DC tại F. Chứng minh tứ giác

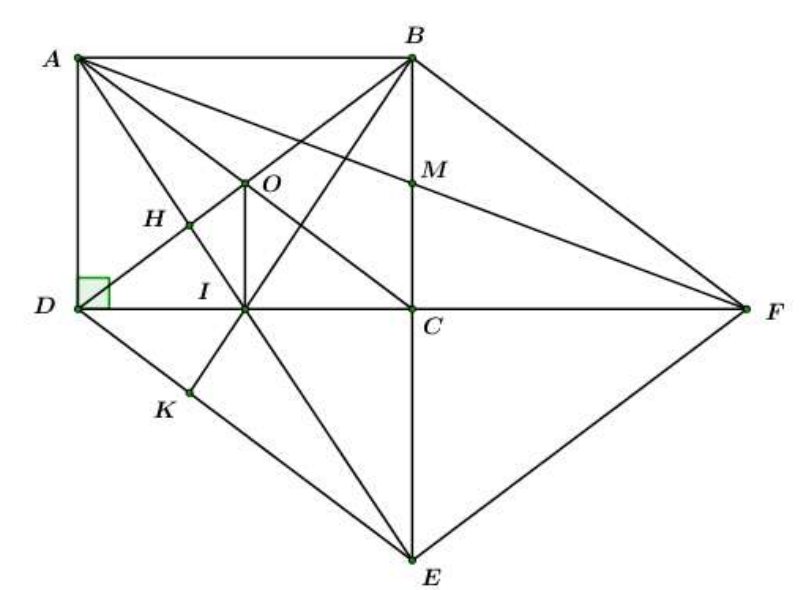
Gọi M là trung điểm của BC. Tia AM cắt tia DC tại F. Chứng minh tứ giác BDEF là hình thoi.

Xét $\Delta ABM$ và $\Delta FCM$ ta có:

$\angle ABM=\angle FCM=90°$

$MB=MC\left(gt\right)$

$\angle AMB=\angle CMF$ (hai góc đối đỉnh)

$\Rightarrow \Delta ABM=\Delta FCM$ (g – c – g)

$\Rightarrow AB=CF$ (hai cạnh tương ứng).

Mà $AB=DC\left(gt\right)\Rightarrow DC=CF.$

Xét tứ giác BDEF ta có:$BE\perp DF=\left\{C\right\}$

$BE\cap DF=\left\{C\right\}$

C là trung điểm của BE, DF

$\Rightarrow$ BDEF là hình thoi. (hình thoi có 2 đường chéo vuông góc với nhau tại trung điểm của mỗi đường).