Tam giác ABC cần thêm điều kiện gì để tứ giác ABBCI là hình

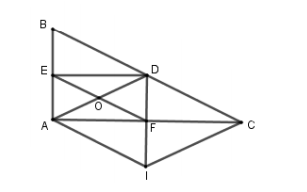
Ta có:$AI//BC$ (do $AI//BD$) nên tứ giác $AICB$ là hình thang.

Để $AICB$ là hình thang cân thì $ABC=ICB$  

Xét tứ giác $AICD$ có $AC$ vuông góc $DI$ tại trung điểm mỗi đường nên là hình thoi.

$\Rightarrow CA$ là tia phân giác góc .

$\Rightarrow ICB=2ACB$

Từ đó $ABC=2ACB$ .

Mà $ABC+ACB=90°\iff ACB=30°$ .

Vậy tam giác $ABC$ cần thêm điều kiện $ACB=30°$ để tứ giác $AICB$ là hình thang cân.

Tam giác $ABC$ vuông tại $A$ có $ACB=30°$ nên $AB=\frac{1}{2}BC$ .

Mà $BC=2AD=2.8=16$ nên $AB=\frac{1}{2}.16=8$ .

Áp dụng định lí Pi-ta-go ta có:$A{B}^2+A{C}^2=B{C}^2\iff 8^2+A{C}^2={16}^2\iff A{C}^2={16}^2-8^2=192\Rightarrow AC=8\sqrt{3}$

Diện tích tam giác: $S_{ABC}=\frac{1}{2}AB.AC=\frac{1}{2}\mathrm{.8.8}\sqrt{3}=32\sqrt{3}$ .