Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Bài tập theo Tuần toán 8- Tuần 26 !!
Cho hình chữ nhật ABCD có AB=4cm, BC=3cm Qua B...
Cho hình chữ nhật ABCD có AB=4cm, BC=3cm Qua B vẽ đường thẳng vuông góc BD với BD cắt DC tại E
Câu hỏi :
Cho hình chữ nhật có Qua vẽ đường thẳng vuông góc với cắt DC tại E
a) Chứng minh từ đó suy ra :
b) Tính
c) Vẽ tại F. Gọi O là giao điểm của AC và BD. Nối OE cắt CF tại I và cắt BC tại K. Chứng minh I là trung điểm
d) Chứng minh thẳng hàng.
Cho hình chữ nhật có Qua vẽ đường thẳng vuông góc với cắt DC tại E
a) Chứng minh từ đó suy ra :
b) Tính
c) Vẽ tại F. Gọi O là giao điểm của AC và BD. Nối OE cắt CF tại I và cắt BC tại K. Chứng minh I là trung điểm
d) Chứng minh thẳng hàng.
* Đáp án
* Hướng dẫn giải
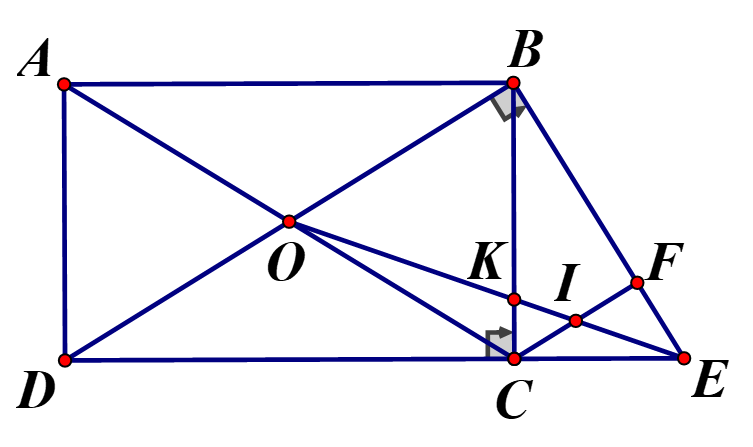
a) Xét và có:
b) Vì là hình chữ nhật nên
Áp dụng hệ thức lượng trong có:
c) Vì
Ta có: có
có
Từ (1) và (2) suy ra
Mà
Vậy I là trung điểm CF
d) Xét và có:
(hệ quả Ta let)
Vậy thẳng hàng.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập theo Tuần toán 8- Tuần 26 !!
Số câu hỏi: 28
Copyright © 2021 HOCTAP247
