Cho tam giác ABC vuông tại A (AB < AC), đường cao AH (H ∈ BC). a) Chứng minh: ∆ ABC đồng dạng với ∆ HBA.

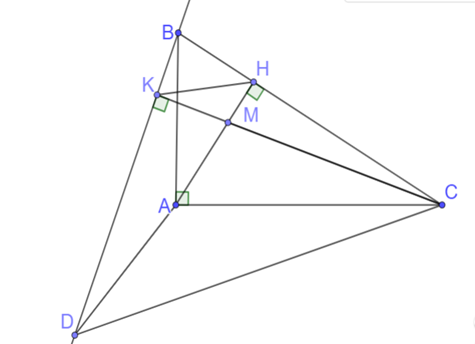
a) Vì ∆ ABC vuông tại A nên $\widehat{BAC}$ = 90°

Vì AH ⊥ BC nên $\widehat{BHA}$= 90°

Xét ∆ ABC và ∆ HBA ta có:

Chung $\widehat{ABC}$

$\widehat{BAC}$ = $\widehat{BHA}$= 90°

Do đó ∆ ABC ᔕ ∆ HBA (g.g)

b) Vì AH ⊥ BC nên $\widehat{CHM}$= 90°

Vì AM ⊥ BD tại K nên $\widehat{CKB}$= 90°

Xét ∆CHM và ∆CBK ta có:

Chung $\widehat{MCH}$

$\widehat{CHM}$ = $\widehat{CKB}$ = 90°

Do đó ∆ CHM ᔕ ∆ CBK (g.g)

$\Rightarrow$ $\frac{CH}{CM}$ = $\frac{CB}{CK}$

$\Rightarrow$ CH. CK = CM. CB (đpcm)

c) Xét ∆CMH và ∆DMK, có:

$\widehat{CHM}=\widehat{DKM}=90°$

$\widehat{CMH}=\widehat{DMK}$ (2 góc đối đỉnh)

⇒ ∆CMH ᔕ ∆DMK (g – g)

⇒ $\frac{MH}{MK}=\frac{CM}{DM}$ (hai cạnh tương ứng)

⇒ $\frac{MH}{CM}=\frac{MK}{DM}$

Xét ∆MHK và ∆MCD, có:

$\frac{MH}{CM}=\frac{MK}{DM}$ (cmt)

$\widehat{HMK}=\widehat{CMD}$ (2 góc đối đỉnh)

⇒ ∆MHK ᔕ ∆MCD (c – g – c)

⇒ $\widehat{CDM}=\widehat{MKH}$ (2 góc tương ứng)

Ta lại có:

$\widehat{CDM}+\widehat{DCH}=90°$ (∆CDH vuông tại H)

$\widehat{HKB}+\widehat{MKH}=\widehat{MKB}=90°$ (hai góc phụ nhau)

Mà $\widehat{CDM}=\widehat{MKH}$ (cmt)

$\Rightarrow \widehat{HKB}=\widehat{DCH}$ hay $\widehat{BKH}$ = $\widehat{BCD}$.