Cho tam giác ABC vuông tại A (AB < AC) và các điểm D, E, F lần lượt là trung điểm
Câu hỏi :
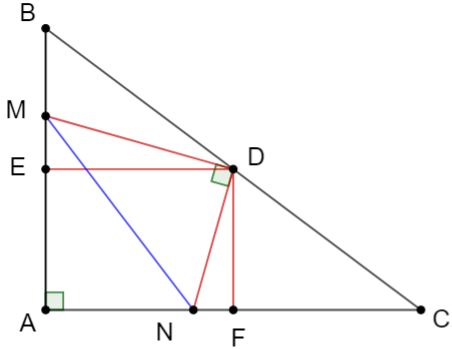
Cho tam giác ABC vuông tại A (AB < AC) và các điểm D, E, F lần lượt là trung điểm của các cạnh BC, AB, AC. Lấy điểm M thuộc đoạn EB (M khác E và B). Kẻ đường thẳng qua D vuông góc với MD tại D, đường thẳng này cắt AC tại N.
a) Chứng minh tam giác DEM đồng dạng tam giác DFN.
b) Chứng minh tam giác DMN đồng dạng tam giác ACB.
c) Chứng minh MN2 = BM2 + CN2.
Cho tam giác ABC vuông tại A (AB < AC) và các điểm D, E, F lần lượt là trung điểm của các cạnh BC, AB, AC. Lấy điểm M thuộc đoạn EB (M khác E và B). Kẻ đường thẳng qua D vuông góc với MD tại D, đường thẳng này cắt AC tại N.
a) Chứng minh tam giác DEM đồng dạng tam giác DFN.
b) Chứng minh tam giác DMN đồng dạng tam giác ACB.
c) Chứng minh MN2 = BM2 + CN2.
* Đáp án
* Hướng dẫn giải
a) +) Xét tam giác BAC có E, D lần lượt là trung điểm của BA và BC nên suy ra ED là đường trung bình của tam giác BAC
Þ ED // AC và
Mà BA ^ AC nên suy ra BA ^ ED
Suy ra
+) Xét tam giác CBA có F, D lần lượt là trung điểm của CA và CB nên suy ra FD là đường trung bình của tam giác BAC
Þ FD // AB và
Mà BA ^ AC nên suy ra AC ^ FD
Suy ra
+) Ta có:
ED // AC, FD // AB mà BA ^ AC nên suy ra ED ^ FD
(1)
Mà (2)
Từ (1) và (2) nên suy ra (Do cùng phụ với góc )
Xét hai tam giác DDEM và DDFN có:
⇒ ∆DEM ᔕ DDFN (g – g)
b) Do DDEM ᔕ DDFN (g – g)
Xét hai tam giác DDMN và DACB có:
⇒ ∆DMN ᔕ DACB (c – g – c)
c) +) Ta có:
MN2 = AM2 + AN2 = (AB - BM)2 + (AC - CN)2
= AB2 - 2AB.BM + BM2 + AC2 - 2AC.CN + CN2
= AB(AB - 2BM) + AC(AC - 2CN) + BM2 + CN2
= AB(2BE - 2BM) + AC(2CF - 2CN) + BM2 + CN2
= 2AB(BE - BM) - 2AC(CN - CF) + BM2 + CN2
= 2AB.EM - 2AC.FN + BM2 + CN2 (3)
+) Lại có:
DDEM ᔕ DDFN (g.g)
Û AB.EM = AC.FN (4)
Thay (4) vào (3) suy ra (3) trở thành
MN2 = BM2 + CN2 (đpcm).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra cuối kì 2 Toán 8 có đáp án ( Mới nhất) !!
Copyright © 2021 HOCTAP247
