Cho ABC có ba góc nhọn (AB < AC), vẽ các đường cao BD và CE. a) Chứng minh ∆ABD ᔕ ∆ACE;

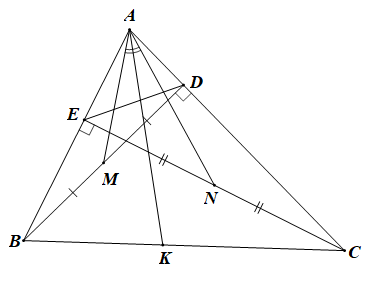
a) Xét ∆ABD và ∆ACE có:

$\widehat{BAC}$ chung,

$\widehat{ADB}=\widehat{AEC}=90°$(gt)

Suy ra ∆ABD ᔕ ∆ACE (g.g)

b) Vì ∆ABD ᔕ ∆ACE (câu a)

$\Rightarrow \frac{AD}{AE}=\frac{AB}{AC}$ (các cặp cạnh tương ứng tỉ lệ)

Xét ∆AED và ∆ACB có

$\frac{AD}{AE}=\frac{AB}{AC}$ ( chứng minh trên)

$\widehat{BAC}$ chung,

Suy ra, ∆AED ᔕ ∆ACB (c.g.c)

$\Rightarrow \widehat{ADE}=\widehat{ABC}$ (hai góc tương ứng)

Mặc khác: $\widehat{ADE}+\widehat{EDC}=180°$(hai góc kề bù)

Do đó $\widehat{ADE}+\widehat{EDC}=\widehat{ABC}+\widehat{EDC}=180°$.

Vậy $\widehat{ABC}+\widehat{EDC}=180°.$

c) Vì ∆ABD ᔕ ∆ACE (câu a)

$\Rightarrow \frac{AB}{AC}=\frac{BD}{CE}$ (tỉ số đồng dạng)

Mà M là trung điểm của BD, N là trung điểm của CE (giả thiết)

Nên ta có: BD = 2BM và CE = 2CN

$\Rightarrow \frac{AB}{AC}=\frac{BD}{CE}=\frac{2BM}{2CN}=\frac{BM}{CN}$

Xét DABM và DACN có:

$\frac{AB}{AC}=\frac{BM}{CN}$ (chứng minh trên),

$\widehat{ABM}=\widehat{ACN}$ (do cùng phụ với $\widehat{BAC}$)

Þ DABM ᔕ DACN (c.g.c)

$\Rightarrow \widehat{BAM}=\widehat{CAN}$ (hai góc tương ứng)

Lại có AK là tia phân giác của $\widehat{MAN}$ (giả thiết)

$\Rightarrow \widehat{MAK}=\widehat{NAK}$ (tính chất tia phân giác của một góc)

Do đó: $\widehat{BAM}+\widehat{MAK}=\widehat{CAN}+\widehat{NAK}$

Hay $\widehat{BAK}=\widehat{KAC}$ 

Þ AK là tia phân giác của $\widehat{BAC}$

Theo tính chất tia phân giác của tam giác ta có:

$\frac{AB}{AC}=\frac{KB}{KC}$ 

Þ KB.AC = KC.AB (điều phải chứng minh).

Vậy KB.AC = KC.AB.