Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Trắc nghiệm chuyên đề Toán 8 Chủ đề 10. Ôn tập và kiểm tra có đáp án !!
Cho a3 + b3 + c3 = 3abc và a...
Cho a3 + b3 + c3 = 3abc và a + b + c ≠ 0.Tính giá trị của biểu thức A= a^2 + b^2 + c^2 / (a+ b+ c)^2
Câu hỏi :
Cho a3 + b3 + c3 = 3abc và a + b + c ≠ 0. Tính giá trị của biểu thức 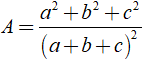
Cho a3 + b3 + c3 = 3abc và a + b + c ≠ 0. Tính giá trị của biểu thức 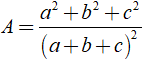
* Đáp án
* Hướng dẫn giải
Ta có: a3 + b3 + c3 = 3abc ⇔ a3 + b3 + c3 - 3abc = 0
⇔ ( a + b )3 + c3 - 3ab( a + b ) - 3abc = 0
⇔ ( a + b )3 + c3 - 3ab( a + b + c ) = 0
⇔ ( a + b + c )3 - 3( a + b )c( a + b + c ) - 3ab( a + b + c ) = 0
⇔ ( a + b + c )( a2 + b2 + c2 - ab - bc - ca ) = 0
⇒ a2 + b2 + c2 - ab - bc - ca = 0 (vì a + b + c ≠ 0. )
⇔ a2 + b2 + c2 = ab + bc + ca.
Khi đó ta có:
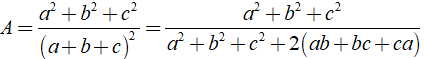
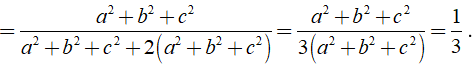
Vậy A= 1/3
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm chuyên đề Toán 8 Chủ đề 10. Ôn tập và kiểm tra có đáp án !!
Số câu hỏi: 83
Copyright © 2021 HOCTAP247
