Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Trắc nghiệm chuyên đề Toán 8 Chủ đề 2: Kiểm tra học kì 2 có đáp án !!
Cho tam giác ABC vuông tại A có AH là...
Cho tam giác ABC vuông tại A có AH là đường cao. Vẽ HD ⊥ AB ( D ∈ AB ). HE ⊥ AC ( E ∈ AC ). AB = 12cm, AC = 16 cm a) Chứng minh : ΔHAC ∼ ΔABC b) Chứng minh : AH2 = AD.AB c) Chứng m...
Câu hỏi :
Cho tam giác ABC vuông tại A có AH là đường cao. Vẽ HD ⊥ AB ( D ∈ AB ). HE ⊥ AC ( E ∈ AC ). AB = 12cm, AC = 16 cm
a) Chứng minh : ΔHAC ∼ ΔABC
b) Chứng minh : AH2 = AD.AB
c) Chứng minh : AD.AB = AE.AC.
Cho tam giác ABC vuông tại A có AH là đường cao. Vẽ HD ⊥ AB ( D ∈ AB ). HE ⊥ AC ( E ∈ AC ). AB = 12cm, AC = 16 cm
a) Chứng minh : ΔHAC ∼ ΔABC
b) Chứng minh : AH2 = AD.AB
c) Chứng minh : AD.AB = AE.AC.
* Đáp án
* Hướng dẫn giải
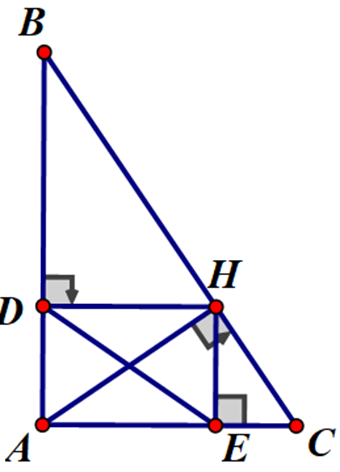
a) Xét ΔHAC và ΔABC có:
∠(ACH ) là góc chung
∠(BAC)= ∠(AHC) = 90o
⇒ ΔHAC ∼ ΔABC (g.g)
b) Xét ΔHAD và ΔBAH có:
∠(DAH ) là góc chung
∠(ADH) = ∠(AHB) = 90o
⇒ ΔHAD ∼ ΔBAH (g.g)
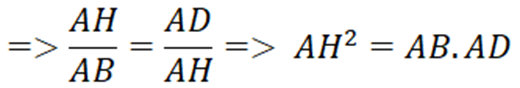
c) Tứ giác ADHE có 3 góc vuông ⇒ ADHE là hình chữ nhật.
⇒ ΔADH= ΔAEH ( c.c.c) ⇒ ∠(DHA)= ∠(DEA)
Mặt khác: ΔHAD ∼ ΔBAH ⇒ ∠(DHA)= ∠(BAH)
∠(DEA)= ∠(BAH)
Xét ΔEAD và ΔBAC có:
∠(DEA)= ∠(BAH)
∠(DAE ) là góc chung
ΔEAD ∼ ΔBAC (g.g)
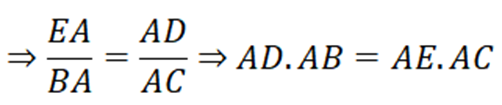
d) ΔEAD ∼ ΔBAC
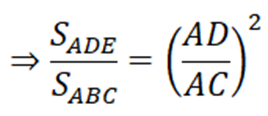
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm chuyên đề Toán 8 Chủ đề 2: Kiểm tra học kì 2 có đáp án !!
Số câu hỏi: 42
Copyright © 2021 HOCTAP247
