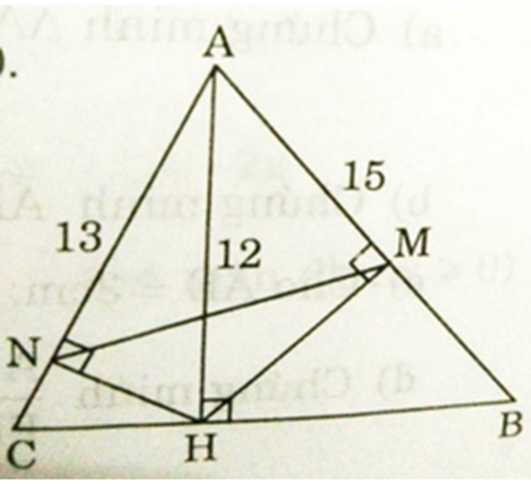
Cho tam giác ABC có ba góc nhọn, biết AB = 15cm, AC = 13cm và đường cao AH = 12cm. Gọi N, M lần lượt là hình chiếu vuông góc của H xuống AC và AB. a) Chứng minh rằng ΔAHN ∼ ΔACH b)...

Câu hỏi :

Cho tam giác ABC có ba góc nhọn, biết AB = 15cm, AC = 13cm và đường cao AH = 12cm. Gọi N, M lần lượt là hình chiếu vuông góc của H xuống AC và AB.

a) Chứng minh rằng ΔAHN ∼ ΔACH

b) Tính độ dài BC

c) Chứng minh ΔAMN ∼ ΔACB

d) Tính MN

* Đáp án

* Hướng dẫn giải

a) Xét ΔANH và ΔAHC có:

∠(NAH) chung

∠(ANH) = ∠(AHN) = 90^o

⇒ ΔANH ∼ ΔAHC (g.g)

b) Ta có :

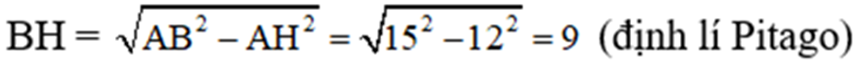
Tương tự : CH = 5 (cm)

⇒ BC = BH + CH = 9 + 5 = 14 (cm)

c) Theo chứng minh trên ta có:

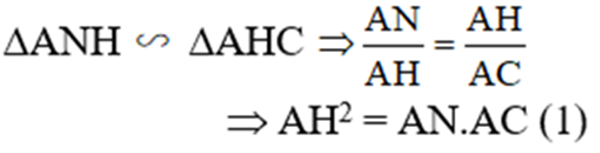
Chứng minh tương tự ta có :

ΔAMH ∼ ΔAHB ⇒ AH₂ = AM.AB (2)

Từ (1) và (2) ⇒ AN.AC = AM.AB (3)

Xét ΔAMN và ΔACB có :

∠A chung

AN.AC = AM.AB

⇒ ΔAMN ∼ ΔACB (c.g.c)

d) Ta có : ΔAMH ∼ ΔAHB

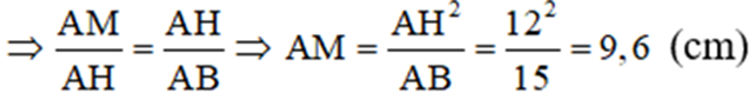
Lại có ΔAMN ∼ ΔACB (cmt)