Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Trắc nghiệm chuyên đề Toán 8 Chủ đề 2: Kiểm tra học kì 2 có đáp án !!
Cho tam giác nhọn ABC, các đường cao AD, BE,...
Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H. a) Chứng minh ΔAEB và ΔAFC đồng dạng. Từ đó suy ra: AF.AB = AE.AC b) Chứng minh ∠AEF = ∠ABC c) Cho AE = 3cm, AB = 6c...
Câu hỏi :
Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh ΔAEB và ΔAFC đồng dạng. Từ đó suy ra: AF.AB = AE.AC
b) Chứng minh ∠AEF = ∠ABC
c) Cho AE = 3cm, AB = 6cm. Chứng minh rằng SABC = 4SAEF
d) Chứng minh

Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh ΔAEB và ΔAFC đồng dạng. Từ đó suy ra: AF.AB = AE.AC
b) Chứng minh ∠AEF = ∠ABC
c) Cho AE = 3cm, AB = 6cm. Chứng minh rằng SABC = 4SAEF
d) Chứng minh

* Đáp án
* Hướng dẫn giải
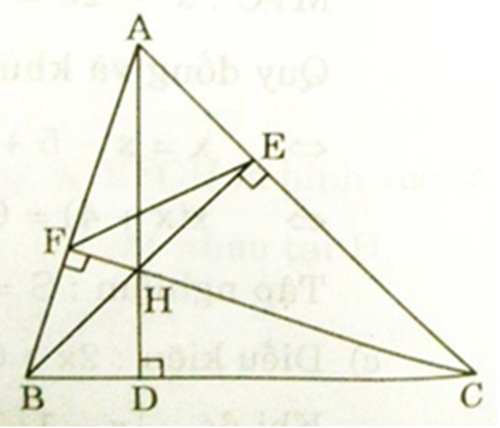
a) Xét ΔAEB và ΔAFC có:
∠AEB = ∠AFC = 90o (gt)
∠A chung
Vậy ΔAEB ∼ ΔAFC (g.g)
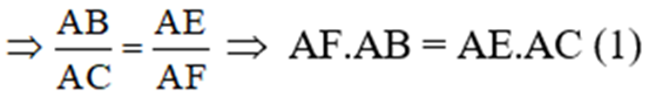
b) Xét ΔAEF và ΔABC có
∠A chung
AF.AB = AE.AC (Cmt)
⇒ ΔAEF ∼ ΔABC (c.g.c)
⇒ ∠AEF = ∠ABC
c) ΔAEF ∼ ΔABC (cmt)
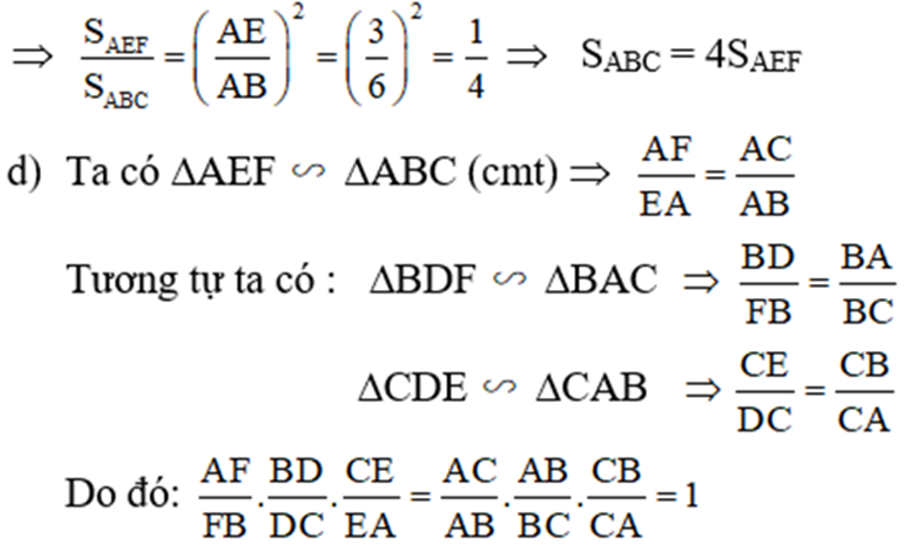
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm chuyên đề Toán 8 Chủ đề 2: Kiểm tra học kì 2 có đáp án !!
Số câu hỏi: 42
Copyright © 2021 HOCTAP247
