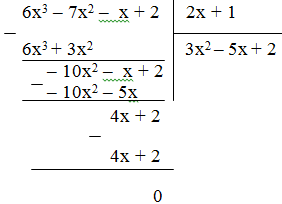Làm tính chia: (6x^3 – 7x^2 – x + 2) : (2x + 1)

* Hướng dẫn giải

Cách 1: Thực hiện phép chia

Vậy (6x3 – 7x2 – x + 2) : (2x + 1) = 3x2 – 5x + 2

Cách 2: Phân tích 6x3 – 7x2 – x + 2 thành (2x + 1).P(x) + R(x)

6x3 – 7x2 – x + 2

= 6x3 + 3x2 – 10x2 – 5x + 4x + 2

(Tách -7x2 = 3x2 – 10x2; -x = -5x + 4x)

= 3x2.(2x + 1) – 5x.(2x + 1) + 2.(2x + 1)

= (3x2 – 5x + 2)(2x + 1)

Vậy (6x3 – 7x2 – x + 2) : (2x + 1) = 3x2 – 5x + 2

Giải thích cách tách:

Vì có 6x3 nên ta cần thêm 3x2 để có thể phân tích thành 3x2(2x + 1). Do đó ta tách -7x2 = 3x2 – 10x2.

Lại có -10x2 nên ta cần thêm -5x để có thể phân tích thành -5x(2x + 1). Do đó ta tách –x = -5x + 4x.

Có 4x, ta cần thêm 2 để có 2.(2x + 1) nên 2 không cần phải tách.