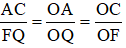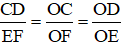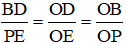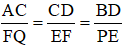Để chia đoạn thẳng AB thành ba đoạn thẳng bằng nhau, người ta đã
Câu hỏi :
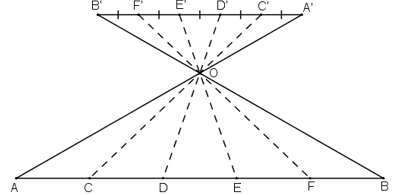
a) Để chia đoạn thẳng AB thành ba đoạn thẳng bằng nhau, người ta đã làm như hình 15.
* Đáp án
* Hướng dẫn giải
a) - Mô tả cách làm:
+ Vẽ đoạn thẳng PQ song song với AB, PQ có độ dài bằng 3 đơn vị.
+ E, F nằm trên PQ sao cho PE = EF = FQ = 1. Xác định giao điểm O của hai đoạn thẳng PB và QA
+ Vẽ các đường thẳng EO, FO cắt AB tại C và D.
Khi đó ta được AC = CD = DB.
- Chứng minh AC = CD = DB:
Theo hệ quả định lý Ta-let ta có:
ΔOAC có FQ // AC (F ∈ OC, Q ∈ OA) ⇒
ΔOCD có EF // CD (E ∈ OD, F ∈ OC) ⇒
ΔODB có PE // BD (P ∈ OB, E ∈ OD) ⇒
Từ 3 đẳng thức trên suy ra
Mà FQ = EF = PE ⇒ AC = CD = DB (đpcm).
b) Tương tự chia đoạn thẳng AB thành 5 đoạn bằng nhau thực hiện như hình vẽ sau
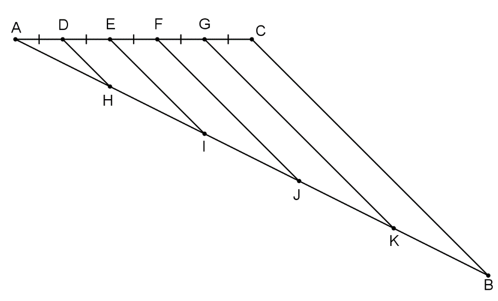
Ngoài cách trên, ta có thể chia một đoạn thẳng thành 5 đoạn bằng nhau bằng cách vẽ thêm một đoạn thẳng AC bằng 5 đơn vị, chia đoạn thẳng AC thành 5 đoạn thẳng bằng nhau, mỗi đoạn bằng 1 đơn vị: AD = DE = EF = FG = GC.
Từ các điểm D, E, F, G ta kẻ các đường thẳng song song với BC, cắt AB tại H, I, J, K. Khi đó ta thu được các đoạn thẳng AH = HI = IJ = JK = KB.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải toán 8: Chương 3: Tam Giác Đồng Dạng !!
Copyright © 2021 HOCTAP247