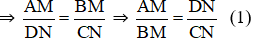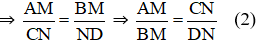Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải toán 8: Chương 3: Tam Giác Đồng Dạng !!
Hình thang ABCD (AB // CD) có AC và BD...
Hình thang ABCD (AB // CD) có AC và BD cắt nhau tại O, AD và BC
Câu hỏi :
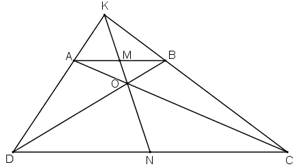
Hình thang ABCD (AB // CD) có AC và BD cắt nhau tại O, AD và BC cắt nhau tại K. Chứng minh rằng OK đi qua trung điểm của các cạnh AB và CD.
* Đáp án
* Hướng dẫn giải
Gọi KO cắt AB, CD lần lượt tại M, N.
ΔKDN có AM // DN (A ∈ KD, M ∈ KN) ⇒ 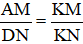
ΔKCN có BM // CN (M ∈ KN, B ∈ KC) ⇒ 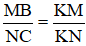
ΔOCN có AM // NC (A ∈ OC, M ∈ ON) ⇒ 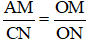
ΔODN có MB // ND (M ∈ ON, B ∈ OD) ⇒ 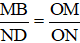
Từ (1) và (2) suy ra 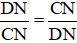
Vậy M, N là trung điểm AB, CD.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải toán 8: Chương 3: Tam Giác Đồng Dạng !!
Số câu hỏi: 93
Copyright © 2021 HOCTAP247