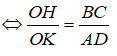Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải Sách Bài Tập Toán 8 Tập 2 !!
Hình thang ABCD (AB // CD) có hai đường chéo...
Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O
Câu hỏi :
Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, K, N, H lần lượt là chân đường vuông góc hạ từ O xuống các cạnh AB, BC, CD, DA. Chứng minh rằng:
* Đáp án
* Hướng dẫn giải
Từ O kẻ đường thẳng song song với AB và CD cắt AD tại E, cắt BC tại F.
Áp dụng kết quả chứng minh ở bài 14 ta có:
OE = OF
Từ đó, ta có:
(1) (hai tam giác có cùng đường cao và hai đáy bằng nhau);
(2)
Từ (1) và (2) suy ra : (3)
Suy ra: OH.AD = OK.BC
⇔
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 2 !!
Số câu hỏi: 715
Copyright © 2021 HOCTAP247