Trang chủ Đề thi & kiểm tra Lớp 8 Toán học Giải Sách Bài Tập Toán 8 Tập 2 !!

Giải Sách Bài Tập Toán 8 Tập 2 !!

Toán học - Lớp 8

Trắc nghiệm Toán 8 Bài 1 Liên hệ giữa thứ tự và phép cộng

Trắc nghiệm Bài 2 Liên hệ giữa thứ tự và phép nhân - Luyện tập - Toán 8

Trắc nghiệm Toán 8 Bài 1 Nhân đơn thức với đa thức

Trắc nghiệm Hình học 8 Bài 1 Tứ giác

Trắc nghiệm Toán 8 Bài 2 Nhân đa thức với đa thức

Trắc nghiệm Toán 8 Bài 3 Những hằng đẳng thức đáng nhớ

Trắc nghiệm Toán 8 Bài 4 Những hằng đẳng thức đáng nhớ (tiếp)

Trắc nghiệm Toán 8 Bài 5 Những hằng đẳng thức đáng nhớ (tiếp)

Trắc nghiệm Toán 8 Bài 6 Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung

Trắc nghiệm Toán 8 Bài 7 Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức

Trắc nghiệm Toán 8 Bài 8 Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử

Trắc nghiệm Toán 8 Bài 9 Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp

Trắc nghiệm Toán 8 Bài 10 Chia đơn thức cho đơn thức

Trắc nghiệm Toán 8 Bài 11 Chia đa thức cho đơn thức

Đề thi học kì 2 môn Toán Lớp 8 - Trường THCS Phạm Công Bình năm học 2019

Trắc nghiệm Toán 8 Bài 12 Chia đa thức một biến đã sắp xếp

Trắc nghiệm Hình học 8 Bài 2 Hình thang

Trắc nghiệm Hình học 8 Bài 3 Hình thang cân

Trắc nghiệm Hình học 8 Bài 4 Đường trung bình của tam giác, của hình thang

Trắc nghiệm Hình học 8 Bài 6 Đối xứng trục

Trắc nghiệm Hình học 8 Bài 7 Hình bình hành

Trắc nghiệm Hình học 8 Bài 8 Đối xứng tâm

Trắc nghiệm Hình học 8 Bài 9 Hình chữ nhật

Trắc nghiệm Hình học 8 Bài 11 Hình thoi

Trắc nghiệm Hình học 8 Bài 12 Hình vuông

Câu 1 : Trong các số -2; -1,5; -1; 0,5; 2/3 ;2 ;3 số nào là nghiệm của mỗi phương trình sau: $y^{2} - 3 = 2 y$

Câu 2 : Trong các số -2; -1,5; -1; 0,5; 2/3 ;2 ;3 số nào là nghiệm của mỗi phương trình sau: t + 3 = 4 - t

Câu 3 : Trong các số -2; -1,5; -1; 0,5; 2/3 ;2 ;3 số nào là nghiệm của mỗi phương trình sau: $\frac{3 x - 4}{2} + 1 = 0$

Câu 4 : Hãy thử lại và cho biết các khẳng định sau có đúng không: $x^{3} + 3 x = 2 x^{2} - 3 x + 1 \Leftrightarrow x = - 1$

Câu 5 : Hãy thử lại và cho biết các khẳng định sau có đúng không: $(z - 2) (z^{2} + 1) = 2 z + 5 \Leftrightarrow z = 3$

Câu 6 : Cho ba biểu thức 5x – 3; $x^{2} - 3 x + 12$ và (x + 1)(x – 3)

Câu 7 : Cho ba biểu thức 5x – 3; $x^{2} - 3 x + 12$ và (x + 1)(x – 3)

Câu 8 : Trong một cửa hàng bán thực phẩm, Tâm thấy cô bán hàng dùng một chiếc cân đĩa. Một bên cô đặt một quả cân 500g, bên đĩa kia, cô đặt hai gói hàng như nhau và ba quả cân nhỏ, mỗi quả 50g thì cân thăng bằng. Nếu mỗi gói hàng là x (gam) thì điều đó có thể được mô tả bởi phương trình nào?

Câu 9 : Thử lại rằng phương trình 2mx - 5 = - x + 6m - 2 luôn luôn nhận x = 3 là nghiệm, dù m lấy bât cứ giá trị nào.

Câu 10 : Cho hai phương trình $x^{2} - 5 x + 6 = 0$ (1) và x + (x - 2)(2x + 1) = 2 (2)

Câu 11 : Cho hai phương trình $x^{2} - 5 x + 6 = 0$ (1) và x + (x - 2)(2x + 1) = 2 (2)

Câu 12 : F

Câu 13 : Tại sao có thể kết luận tập nghiệm của phương trình $\sqrt{x} + 1 = 2 \sqrt{- x}$ là ∅?

Câu 14 : Chứng minh rằng phương trình x + |x| = 0 nghiệm đúng với mọi x ≤ 0

Câu 15 : Cho phương trình $(m^{2} + 5 m + 4) x^{2} = m + 4$ , trong đó m là một số. Chứng minh rằng: Khi m = - 4, phương trình nghiệm đúng với mọi giá trị của ẩn

Câu 16 : Cho phương trình $(m^{2} + 5 m + 4) x^{2} = m + 4$ , trong đó m là một số. Chứng minh rằng: Khi m = - l, phương trình nghiệm vô nghiệm.

Câu 17 : Cho phương trình $(m^{2} + 5 m + 4) x^{2} = m + 4$ , trong đó m là một số. Chứng minh rằng: Khi m = - 2 hoặc m = -3, phương trình vô nghiệm.

Câu 18 : Cho phương trình $(m^{2} + 5 m + 4) x^{2} = m + 4$ , trong đó m là một số. Chứng minh rằng: Khi m = 0 phương trình nhận x = l và x = - l là nghiệm.

Câu 19 : Bằng quy tắc chuyển vế, giải các phương trình sau: x – 2,25 = 0,75

Câu 20 : Bằng quy tắc chuyển vế, giải các phương trình sau: 19,3 = 12 – x

Câu 21 : Bằng quy tắc chuyển vế, giải các phương trình sau: 4,2 = x + 2,1

Câu 22 : Bằng quy tắc chuyển vế, giải các phương trình sau: 3,7 – x = 4

Câu 23 : Bằng quy tắc nhân, tìm giá trị gần đúng nghiệm của các phương trình sau (làm tròn đến chữ số thập phân thứ ba). 2x = $\sqrt{13}$

Câu 24 : Bằng quy tắc nhân, tìm giá trị gần đúng nghiệm của các phương trình sau (làm tròn đến chữ số thập phân thứ ba). x $\sqrt{2}$ = 4 $\sqrt{3}$

Câu 25 : Bằng quy tắc nhân, tìm giá trị gần đúng nghiệm của các phương trình sau (làm tròn đến chữ số thập phân thứ ba). –5x = 1 + $\sqrt{5}$

Câu 26 : Tìm giá trị của m sao cho phương trình sau đây nhận x = -2 là nghiệm: 2x + m = x – 1

Câu 27 : Tìm giá trị của k, biết rắng một trong hai phương trình sau đây nhận x = 5 là nghiệm, phương trình còn lại nhận x = -1 là nghiệm: 2x = 10 và 3 – kx = 2

Câu 28 : Giải các phương trình sau: 7x + 21 = 0

Câu 29 : Giải các phương trình sau: 5x – 2 = 0

Câu 30 : Giải các phương trình sau: 12 – 6x = 0

Câu 31 : Giải các phương trình sau: -2x + 14 = 0

Câu 32 : Giải các phương trình sau: 0,25x + 1,5 = 0

Câu 33 : Giải các phương trình sau: 6,36 – 5,3x = 0

Câu 34 : Giải các phương trình sau: 4/3 x - 5/6 = 1/2

Câu 35 : Giải các phương trình sau: -5/9 x + 1 = 2/3 x – 10

Câu 36 : Giải các phương trình sau: 3x + 1 = 7x – 11

Câu 37 : Giải các phương trình sau: 5 – 3x = 6x + 7

Câu 38 : Giải các phương trình sau: 11 – 2x = x – 1

Câu 39 : Giải các phương trình sau: 15 – 8x = 9 – 5x

Câu 40 : Chứng tỏ rằng các phương trình sau đây vô nghiệm: 2(x + 1) = 3 + 2x

Câu 41 : Chứng tỏ rằng các phương trình sau đây vô nghiệm: 2(1 – 1,5x) + 3x = 0

Câu 42 : Chứng tỏ rằng các phương trình sau đây vô nghiệm: |x| = -1

Câu 43 : Cho phương trình $(m^{} - 4) x + 2 = m$ . Giải phương trình trong mỗi trường hợp sau: m = 2

Câu 44 : Cho phương trình $(m^{} - 4) x + 2 = m$ . Giải phương trình trong mỗi trường hợp sau: m = -2

Câu 45 : Cho phương trình $(m^{} - 4) x + 2 = m$ . Giải phương trình trong mỗi trường hợp sau: m = -2,2

Câu 46 : Giải các phương trình sau: 1,2 – (x – 0,8) = -2(0,9 + x)

Câu 47 : Giải các phương trình sau: 2,3x – 2(0,7 + 2x) = 3,6 – 1,7x

Câu 48 : Giải các phương trình sau: 3(2,2 – 0,3x) = 2,6 + (0,1x – 4)

Câu 49 : Giải các phương trình sau: 3,6 – 0,5(2x + 1) = x – 0,25(2 – 4x)

Câu 50 : Giải các phương trình sau $\frac{x - 3}{5} = 6 - \frac{1 - 2 x}{3}$

Câu 51 : Giải các phương trình sau: $\frac{3 x - 2}{6} - 5 = \frac{3 - 2 (x + 7)}{4}$

Câu 52 : Giải các phương trình sau: $2 (x + \frac{3}{5}) = 5 - (\frac{13}{5} + x)$

Câu 53 : Giải các phương trình sau: $\frac{7 x}{8} - 5 (x - 9) = \frac{20 x + 1, 5}{6}$

Câu 54 : Tìm điều kiện của x để giá trị mỗi phân thức sau xác định: $A = \frac{3 x + 2}{2 (x - 1) - 3 (2 x + 1)}$

Câu 55 : Tìm điều kiện của x để giá trị mỗi phân thức sau xác định: $B = \frac{(0, 5 (x + 3) - 2)}{(1, 2 (x + 0, 7)) - 4 (0, 6 x + 0, 9))}$

Câu 56 : Giải các phương trình sau: $\frac{5 (x - 1) + 2}{6} - \frac{7 x - 1}{4} = \frac{2 (2 x + 1)}{7} - 5$

Câu 57 : Giải các phương trình sau: $\frac{3 (x - 3)}{4} + \frac{4 x - 10, 5}{10} = \frac{3 (x + 1)}{5} + 6$

Câu 58 : Giải các phương trình sau: $\frac{2 (3 x + 1) + 1}{4} - 5 = \frac{2 (3 x - 1)}{5} - \frac{3 x + 2}{10}$

Câu 59 : Giải các phương trình sau: $\frac{x + 1}{3} + \frac{3 (2 x + 1)}{4} = \frac{2 x + 3 (x + 1)}{6} + \frac{7 + 12 x}{12}$

Câu 60 : Tìm giá trị của k sao cho: Phương trình (2x + 1)(9x + 2k) – 5(x + 2) = 40 có nghiệm x = 2.

Câu 61 : Tìm giá trị của k sao cho: Phương trình 2(2x + 1) + 18 = 3(x + 2)(2x + k) có nghiệm x = 1.

Câu 62 : Tìm các giá trị của x sao cho hai biểu thức A và B cho sau đây có giá trị bằng nhau: A = (x – 3)(x + 4) – 2(3x – 2); B = ${(x - 4)}^{2}$

Câu 63 : Tìm các giá trị của x sao cho hai biểu thức A và B cho sau đây có giá trị bằng nhau: A = (x + 2)(x – 2) + 3 $x^{2}$ ; B = ${(2 x + 1)}^{2}$ + 2x

Câu 64 : Tìm các giá trị của x sao cho hai biểu thức A và B cho sau đây có giá trị bằng nhau: A = (x – 1)( $x^{2}$ + x + 1) – 2x; B = x(x – 1)(x + 1)

Câu 65 : Tìm các giá trị của x sao cho hai biểu thức A và B cho sau đây có giá trị bằng nhau: A = ${(x + 1)}^{3}$ – ${(x - 2)}^{3}$ ; B = (3x – 1)(3x + 1)

Câu 66 : Giải các phương trình sau: $\frac{2 x}{3} + \frac{2 x - 1}{6} = 4 - \frac{x}{3}$

Câu 67 : Giải các phương trình sau: $\frac{x - 1}{2} + \frac{x - 1}{4} = 1 - \frac{2 (x - 1)}{2}$

Câu 68 : Giải các phương trình sau: $\frac{2 - x}{2001} - 1 = \frac{1 - x}{2002} - \frac{x}{2003}$

Câu 69 : Cho hai phương trình:

Câu 70 : Cho hai phương trình:

Câu 71 : Cho hai phương trình:

Câu 72 : Bằng cách đặt ẩn phụ theo hướng dẫn, giải các phương trình sau: $\frac{6 (16 x + 3)}{7} - 8 = \frac{3 (16 x + 3)}{7} + 7$

Câu 73 : Bằng cách đặt ẩn phụ theo hướng dẫn, giải các phương trình sau: $(\sqrt{2} + 2) (x \sqrt{2} - 1) = 2 x \sqrt{2} - \sqrt{2}$

Câu 74 : Bằng cách đặt ẩn phụ theo hướng dẫn, giải các phương trình sau: $0, 05 (\frac{2 x - 2}{2009} + \frac{2 x}{2010} + \frac{2 x + 2}{2011}) = 3, 3 - (\frac{x - 1}{2009} + \frac{x}{2010} + \frac{x + 1}{2011})$

Câu 75 : Giải các phương trình sau: (4x – 10)(24 + 5x) = 0

Câu 76 : Giải các phương trình sau: (3,5 – 7x)(0,1x + 2,3) = 0

Câu 77 : Giải các phương trình sau: $(3 x - 2) [\frac{2 (x + 3)}{7} - \frac{4 x - 3}{5}] = 0$

Câu 78 : Giải các phương trình sau: $(3, 3 - 11 x) [\frac{7 x + 2}{5} + \frac{2 (1 - 3 x)}{3}] = 0$

Câu 79 : Dùng máy tính bỏ túi để tính giá trị gần đúng các nghiệm của mỗi phương trình sau, làm tròn đến chữ số thập phân thứ ba. ( $\sqrt{3}$ - x $\sqrt{5}$ )(2x $\sqrt{2}$ + 1) = 0

Câu 80 : Dùng máy tính bỏ túi để tính giá trị gần đúng các nghiệm của mỗi phương trình sau, làm tròn đến chữ số thập phân thứ ba. (2x - $\sqrt{7}$ )(x $\sqrt{10}$ + 3) = 0

Câu 81 : Dùng máy tính bỏ túi để tính giá trị gần đúng các nghiệm của mỗi phương trình sau, làm tròn đến chữ số thập phân thứ ba. (2 – 3x $\sqrt{5}$ )(2,5x + $\sqrt{2}$ ) = 0

Câu 82 : Dùng máy tính bỏ túi để tính giá trị gần đúng các nghiệm của mỗi phương trình sau, làm tròn đến chữ số thập phân thứ ba. ( $\sqrt{13}$ + 5x)(3,4 – 4x $\sqrt{1, 7}$ ) =

Câu 83 : Giải các phương trình sau: (x – 1)(5x + 3) = (3x – 8)(x – 1)

Câu 84 : Giải các phương trình sau: 3x(25x + 15) – 35(5x + 3) = 0

Câu 85 : Giải các phương trình sau: (2 – 3x)(x + 11) = (3x – 2)(2 – 5x)

Câu 86 : Giải các phương trình sau: ${(2 x - 1)}^{2}$ + (2 – x)(2x – 1) = 0

Câu 87 : Giải các phương trình sau: (x + 2)(3 – 4x) = $x^{2}$ + 4x + 4

Câu 88 : Giải các phương trình sau: $x^{2}$ + (x + 2)(11x - 7) = 4

Câu 89 : Giải các phương trình sau: (x – 1)( $x^{2}$ + 5x – 2) – ( $x^{3}$ – 1) = 0

Câu 90 : Giải các phương trình sau: $x^{3}$ + 1 = x(x + 1)

Câu 91 : Giải các phương trình bậc hai sau đây bằng cách đưa về dạng phương trình tích: $x^{2}$ – 3x + 2 = 0

Câu 92 : Giải các phương trình bậc hai sau đây bằng cách đưa về dạng phương trình tích: – $x^{2}$ + 5x – 6 = 0

Câu 93 : Giải các phương trình bậc hai sau đây bằng cách đưa về dạng phương trình tích: 2 $x^{2}$ + 5x + 3 = 0

Câu 94 : Giải các phương trình bậc hai sau đây bằng cách đưa về dạng phương trình tích: 4 $x^{2}$ – 12x + 5 = 0

Câu 95 : Giải các phương trình bằng cách đưa về dạng phương trình tích: (x - $\sqrt{2}$ ) + 3( $x^{2}$ – 2) = 0

Câu 96 : Giải các phương trình bằng cách đưa về dạng phương trình tích: $x^{2}$ – 5 = (2x - $\sqrt{5}$ )(x + $\sqrt{5}$ )

Câu 97 : Cho phương trình (3x + 2k – 5)(x – 3k + 1) = 0, trong đó k là một số. Với mỗi giá trị của k tìm được trong câu a, hãy giải phương trình đã cho.

Câu 98 : Cho phương trình (3x + 2k – 5)(x – 3k + 1) = 0, trong đó k là một số. Tìm các giá trị của k sao cho một trong các nghiệm của phương trình là x = 1.

Câu 99 : Biết x = - 2 là một trong các nghiệm của phương trình: $x^{3} + a x^{2} - 4 x - 4 = 0$ . Xác định giá trị của a.

Câu 100 : Cho biểu thức hai biến: f(x; y) = (2x – 3y + 7)(3x + 2y – 1). Tìm các giá trị của y sao cho phương trình (ẩn x) f(x;y) = 0, nhận x = -3 làm nghiệm.

Câu 101 : Biết x = - 2 là một trong các nghiệm của phương trình: $x^{3} + a x^{2} - 4 x - 4 = 0$ . Với a tìm được ở câu a, tìm các nghiêm còn lại của phương trình bằng cách đưa phương trình đã cho về dạng phương trình tích.

Câu 102 : Cho biểu thức hai biến: f(x; y) = (2x – 3y + 7)(3x + 2y – 1). Tìm các giá trị của x sao cho phương trình (ẩn y) f(x;y) = 0; nhận y = 2 làm nghiệm.

Câu 103 : Em hãy chọn khẳng định đúng trong hai khẳng định sau đây:

Câu 104 : Khi giải phương trình $\frac{2 - 3 x}{- 2 x - 3} = \frac{3 x + 2}{2 x + 1}$ , bạn Hà làm như sau:

Câu 105 : Các khẳng định sau đây đúng hay sai:

Câu 106 : Giải các phương trình sau: $\frac{1 - x}{x + 1} + 3 = \frac{2 x + 3}{x + 1}$

Câu 107 : Giải các phương trình sau: $\frac{{(x + 2)}^{2}}{2 x - 3} - 1 = \frac{x^{2} + 10}{2 x - 3}$

Câu 108 : Giải các phương trình sau: $\frac{5 x - 2}{2 - 2 x} + \frac{2 x - 1}{2} = 1 - \frac{x^{2} + x - 3}{1 - x}$

Câu 109 : Giải các phương trình sau: $\frac{5 - 2 x}{3} + \frac{(x + 1) (x - 1)}{3 x - 1} = \frac{(x + 2) (1 - 3 x)}{9 x - 3}$

Câu 110 : Tìm x sao cho biểu thức $\frac{2 x^{2} - 3 x - 2}{x^{2} - 4}$ bằng 2.

Câu 111 : Tìm x sao cho giá trị của hai biểu thức sau bằng nhau: $\frac{6 x - 1}{3 x + 2} v à \frac{2 x + 5}{x - 3}$

Câu 112 : Tìm y sao cho giá trị của hai biểu thức sau bằng nhau: $\frac{y + 5}{y - 1} - \frac{y + 1}{y - 3} v à \frac{- 8}{(y - 1) (y - 3)}$

Câu 113 : Giải các phương trình sau: $\frac{1 - 6 x}{x - 2} + \frac{9 x + 4}{x + 2} = \frac{x (3 x - 2) + 1}{x^{2} - 4}$

Câu 114 : Giải các phương trình sau: $\frac{2}{x - 1} + \frac{2 x + 3}{x^{2} + x + 1} = \frac{(2 x - 1) (2 x + 1)}{x^{3} - 1}$

Câu 115 : Giải các phương trình sau: $1 + \frac{x}{3 - x} = \frac{5 x}{(x + 2) (3 - x)} + \frac{2}{x + 2}$

Câu 116 : Giải các phương trình sau: $\frac{x^{3} - {(x - 1)}^{3}}{(4 x + 3) (x - 5)} = \frac{7 x - 1}{4 x + 3} - \frac{x}{x - 5}$

Câu 117 : Giải các phương trình sau: $\frac{2 x + 1}{x - 1} = \frac{5 (x - 1)}{x + 1}$

Câu 118 : Giải các phương trình sau: $\frac{x - 3}{x - 2} + \frac{x - 2}{x - 4} = - 1$

Câu 119 : Giải các phương trình sau: $\frac{1}{x - 1} + \frac{2 x^{2} - 5}{x^{3} - 1} = \frac{4}{x^{2} + x + 1}$

Câu 120 : Giải các phương trình sau: $\frac{13}{(x - 3) (2 x + 7)} + \frac{1}{2 x + 7} = \frac{6}{x^{2} - 9}$

Câu 121 : Cho phương trình ẩn x: $\frac{x + a}{a - x} + \frac{x - a}{a + x} = \frac{a (3 a + 1)}{a^{2} - x^{2}}$

Câu 122 : Cho phương trình ẩn x: $\frac{x + a}{a - x} + \frac{x - a}{a + x} = \frac{a (3 a + 1)}{a^{2} - x^{2}}$

Câu 123 : Cho phương trình ẩn x: $\frac{x + a}{a - x} + \frac{x - a}{a + x} = \frac{a (3 a + 1)}{a^{2} - x^{2}}$

Câu 124 : Cho phương trình ẩn x: $\frac{x + a}{a - x} + \frac{x - a}{a + x} = \frac{a (3 a + 1)}{a^{2} - x^{2}}$

Câu 125 : Giải các phương trình: $\frac{2}{x + \frac{1}{1 + \frac{x + 1}{x - 2}}} = \frac{6}{3 x - 1}$

Câu 126 : Giải các phương trình: $\frac{\frac{x + 1}{x - 1} - \frac{x - 1}{x + 1}}{1 + \frac{x + 1}{x - 1}} = \frac{x - 1}{2 (x + 1)}$

Câu 127 : Giải các phương trình: $\frac{5}{x} + \frac{4}{x + 1} = \frac{3}{x + 2} + \frac{2}{x + 3}$

Câu 128 : Tổng hai số bằng 80, hiệu của chúng bằng 14. Tìm hai số đó.

Câu 129 : Tổng, hai số bằng 90, số này gấp đôi số kia Tìm hai số đó.

Câu 130 : Hiệu của hai số bằng 22, số này gấp đôi số kia. Tìm hai số đó, biết rằng: Hai số nêu trong bài là hai số dương.

Câu 131 : Hiệu của hai số bằng 22, số này gấp đôi số kia. Tìm hai số đó, biết rằng: Hai số nêu trong bài là hai số tùy ý.

Câu 132 : Hiệu của hai số bằng 18, tỉ số giữa chúng bằng 5/8 . Tìm hai số đó biết rằng: Hai số nêu trong bài là hai số dương.

Câu 133 : Hiệu của hai số bằng 18, tỉ số giữa chúng bằng 5/8 . Tìm hai số đó biết rằng: Hai số nêu trong bài là hai số tùy ý.

Câu 134 : Hai số nguyên dương có tỉ số giữa số thứ nhất và số thứ hai bằng 3/5. Nếu lấy số thứ nhất chia cho 9, số thứ hai chia cho 6 thì thương của phép chia số thứ nhất cho 9 bé hơn thương của phép chia số thứ hai cho 6 là 3 đơn vị. Tìm hai số đó biết rằng các phép chia nói trên đều là phép chia hết.

Câu 135 : Thùng thứ nhất chứa 60 gói kẹo, thùng thứ hai chứa 80 gói kẹo. Người ta lấy ra từ thùng thứ hai số gói kẹo nhiều gấp ba lần số gói kẹo lấy ra từ thùng thứ nhất. Hỏi có bao nhiêu gói kẹo lấy ra từ thùng thứ nhất, biết rằng số gói kẹo còn lại trong thùng thứ nhất nhiều gấp hai lần số gói kẹo trong thùng thứ hai.

Câu 136 : Một ô tô đi từ Hà Nội đến Thanh Hóa với vận tốc 40km/h. Sau 2 giờ nghỉ ở Thanh Hóa, ô tô lại từ Thanh Hóa về Hà Nội với vận tốc 30km/h. Tổng thời gian cả đi và về là 10 giờ 45 phút (kể cả thời gian nghỉ Tại ở Thanh Hóa). Tính quãng đường Hà Nội - Thanh Hóa.

Câu 137 : Trong một buổi lao động, lớp 8A gồm 40 học sinh chia thành hai tốp: tốp thứ nhất trồng cây và tốp thứ hai làm vệ sinh. Tốp trồng cây đông hơn tốp làm vệ sinh là 8 người. Hỏi tốp trồng cây có bao nhiêu học sinh?

Câu 138 : Bài toán cổ Hy Lạp

Câu 139 : Một số tự nhiên lẻ có hai chữ số và chia hết cho 5. Hiệu của số đó và chữ số hàng chục của nó bằng 68. Tìm số đó.

Câu 140 : Ông của Bình hơn Bình 58 tuổi. Nếu cộng tuổi của bố Bình và hai lần tuổi của Bình thì bằng tuổi của ông và tổng số tuổi của ba người bằng 130. Hãy tính tuổi của Bình.

Câu 141 : Một phân số có tử số bé hơn mẫu số là 11. Nếu tăng tử số lên 3 đơn vị và giảm mẫu số đi 4 đơn vị thì được một phân số bằng 3/4 .Tìm phân số ban đầu.

Câu 142 : Một số thập phân có phần nguyên là số có một chữ số. Nếu viết thêm chữ số 2 vào bên trái số đó, sau đó chuyển dấu phẩy sang trái một chữ số thì được số mới bằng 9/10 số ban đầu. Tìm số thập phân ban đầu.

Câu 143 : Một ô tô đi từ Hà Nội lúc 8 giờ sáng, dự kiến đến Hải Phòng vào lúc 10 giờ 30 phút. Nhưng mỗi giờ ô tô đã đi chậm hơn so với dự kiến là 10km nên mãi đến 11 giờ 20 phút xe mới tới Hải Phòng. Tính quãng đường Hà Nội - Hải Phòng.

Câu 144 : Một tàu chở hàng từ ga Vinh về ga Hà Nội. Sau đó 1,5 giờ, một tàu khách xuất phát từ ga Hà Nội đi Vinh với vận tốc lớn hơn vận tốc tàu chở hàng là 7km/h. Khi tàu khách đi được 4 giờ thì nó còn cách tàu hàng là 25km. Tính vận tốc mỗi tàu, biết rằng hai ga cách nhau 319km.

Câu 145 : Một người đi xe đạp từ A đến B. Lúc đầu, trên đoạn đường đá, người đó đi với vận tốc 10km/h. Trên đoạn đường còn lại là đường nhựa, dài gấp rưỡi đoạn đường đá, người đó đi với vận tốc 15km/h. Sau 4 giờ, người đó đến B. Tính độ dài đoạn đường AB.

Câu 146 : Một miếng hợp kim đồng và thiếc có khối lượng là 12kg, chứa 45% đồng. Hỏi phải thêm vào đó bao nhiêu thiếc nguyên chất để được hợp kim mới có chứa 40% đồng.

Câu 147 : Bánh trước của máy kéo có chu vi là 2,5m, bánh sau có chu vi là 4m. Khi máy kéo đi từ A đến B, bánh trước quay nhiều hơn bánh sau 15 vòng. Tính khoảng cách AB.

Câu 148 : Một cửa hàng bán một máy vi tính với giá 6,5 triệu đồng chưa kể thuế giá trị gia tăng (VAT). Anh Trọng mua máy vi tính đó cùng với một môđem ngoài và phải trả tổng cộng là 7,546 triệu đồng, trong đó đã tính cả 10% thuế VAT. Hỏi tiền mua chiếc môđem (không kể VAT) là bao nhiêu?

Câu 149 : Cho hai biểu thức A = 5/(2m + 1) và B = 4/(2m - 1) . Hãy tìm các giá trị của m để hai biểu thức ấy có giá trị thỏa mãn hệ thức: 2A + 3B = 0

Câu 150 : Cho hai biểu thức A = 5/(2m + 1) và B = 4/(2m - 1) . Hãy tìm các giá trị của m để hai biểu thức ấy có giá trị thỏa mãn hệ thức: A.B = A + B

Câu 151 : Tính gần đúng nghiệm của các phương trình sau, làm tròn đến chữ số thập phân thứ hai. (x $\sqrt{13}$ + $\sqrt{5}$ )( $\sqrt{7}$ – x $\sqrt{3}$ ) = 0

Câu 152 : Tính gần đúng nghiệm của các phương trình sau, làm tròn đến chữ số thập phân thứ hai. (x $\sqrt{2, 7}$ – 1,54)( $\sqrt{1, 02}$ + x $\sqrt{3, 1}$ ) = 0

Câu 153 : Giải các phương trình sau: $\frac{(9 x - 0, 7)}{4} - \frac{(5 x - 1, 5)}{7} = \frac{(7 x - 1, 1)}{3} - \frac{5 (0, 4 - 2 x)}{6}$

Câu 154 : Giải các phương trình sau: $\frac{3 x - 1}{x - 1} - \frac{2 x + 5}{x + 3} = 1 - \frac{4}{(x - 1) (x + 3)}$

Câu 155 : Giải các phương trình sau: $\frac{3}{4 (x - 5)} + \frac{15}{50 - 2 x^{2}} = \frac{7}{6 (x + 5)}$

Câu 156 : Giải các phương trình sau: $\frac{8 x^{2}}{3 (1 - 4 x^{2})} = \frac{2 x}{6 x - 3} - \frac{1 + 8 x}{4 + 8 x}$

Câu 157 : Cho phương trình (ẩn x): $4 x^{2} - 25 + k^{2} + 4 k x = 0$ . Giải phương trình với k = 0

Câu 158 : Cho phương trình (ẩn x): $4 x^{2} - 25 + k^{2} + 4 k x = 0$ . Giải phương trình với k = -3

Câu 159 : Cho phương trình (ẩn x): $4 x^{2} - 25 + k^{2} + 4 k x = 0$ . Tìm các giá trị của k sao cho phương trình nhận x = - 2 làm nghiệm

Câu 160 : Giải các phương trình sau: $(x + 2) (x^{2} - 3 x + 5) = (x + 2) x^{2}$

Câu 161 : Giải các phương trình sau: 2 $x^{2}$ – x = 3 – 6x

Câu 162 : Giải các phương trình sau: $\frac{- 7 x^{2} + 4}{x^{3} + 1} = \frac{5}{x^{2} - x + 1} - \frac{1}{x + 1}$

Câu 163 : Giải các phương trình sau: $\frac{x - 2}{x + 2} - \frac{3}{x - 2} = \frac{2 (x - 11)}{x^{2} - 4}$

Câu 164 : Số nhà của Khanh là một số tự nhiên có hai chữ số. Nếu thêm chữ số 5 vào bên trái số đó thì được một số kí hiệu là A. Nếu thêm chữ số 5 vào bên phải số đó thì được một số kí hiệu là B. Tìm số nhà của Khanh, biết rằng A - B = 153.

Câu 165 : Một đội thợ mỏ lập kế hoạch khai thác than, theo đó mỗi ngày phải khai thác được 50 tấn than. Khi thực hiện, mỗi ngày đội khai thác được 57 tấn than. Do đó, đội đã hoàn thành kế hoạch trước một ngày và còn vượt mức 13 tấn than. Hỏi theo kế hoạch, đội phải khai thác bao nhiêu tấn than?

Câu 166 : Hai ô tô cùng khởi hành từ Lạng Sơn và Hà Nội, quãng đường dài 163km. Trong 43km đầu, hai xe cùng vận tốc. Nhưng sau đó chiếc xe thứ nhất tăng vận tốc lên gấp 1,2 lần vận tốc ban đầu, trong khi đó xe thứ hai vẫn duy trì vận tốc cũ. Do đó xe thứ nhất đến Hà Nội sớm hơn xe thứ hai là 40 phút. Tính vận tốc ban đầu của hai xe.

Câu 167 : Một đoàn tàu hỏa từ Hà Nội đi thành phố Hồ Chí Minh. 1 giờ 48 phút sau, một tàu hỏa khác khởi hành từ Nam Định đi thành phố Hồ Chí Minh với vận tốc nhỏ hơn vận tốc của đoàn tàu thứ nhất là 5km/h. Hai đoàn tàu gặp nhau (ở ga nào đó) sau 4 giờ 48 phút kể từ khi đoàn tàu thứ nhất khởi hành. Tính vận tốc của mỗi tàu biết rằng ga Nam Định nằm trên đường từ Hà Nội đi thành phố Hồ Chí Minh và cách Hà Nội 87km

Câu 168 : Lúc 7h sáng, một ca nô xuôi dòng từ bến A đến bến B, cách nhau 36km rồi ngay lập tức quay trở về bến A lúc 11 giờ 30 phút. Tính vận tốc của ca nô khi xuôi dòng biết rằng vận tốc của nước chảy là 6km/h.

Câu 169 : Giải các phương trình sau $\frac{13}{(2 x + 7) (x - 3)} + \frac{1}{2 x + 7} = \frac{6}{x^{2} - 9}$

Câu 170 : Giải các phương trình sau ${(1 - \frac{2 x - 1}{x + 1})}^{3} + 6 {(1 - \frac{2 x - 1}{x + 1})}^{2} = \frac{12 (2 x - 1)}{x + 1} - 20$

Câu 171 : Cho ba số a, b và c đôi một phân biệt. Giải phương trình $\frac{x}{(a - b) (a - c)} + \frac{x}{(b - a) (b - c)} + \frac{z}{(c - a) (c - b)} = 2$

Câu 172 : Cho số a và ba số b, c, d khác a và thỏa mãn điều kiện c + d = 2b. Giải phương trình $\frac{x}{(a - b) (a - c)} - \frac{2 x}{(a - b) (a - d)} + \frac{3 x}{(a - c) (a - d)} = \frac{4 a}{(a - c) (a - d)}$

Câu 173 : Cần phải thêm vào tử và mẫu của phân số 13/18 với cùng một số tự nhiên nào để được phân số 4/5?

Câu 174 : Cách đây 10 năm, tuổi của người thứ nhất gấp 3 lần tuổi của người thứ hai. Sau đây 2 năm, tuổi của người thứ hai bằng nửa tuổi của người thứ nhất. Hỏi hiện nay, tuổi của mỗi người là bao nhiêu ?

Câu 175 : Mỗi khẳng định sau đây đúng hay sai?

Câu 176 : Chuyển các khẳng định sau về dạng bất đẳng thức và cho biết khẳng định đó đúng hay sai?

Câu 177 : Đặt dấu $<, >, \geq, \leq$ vào ô vuông cho thích hợp:

Câu 178 : Đặt dấu $<, >, \geq, \leq$ vào ô vuông cho thích hợp:

Câu 179 : Đặt dấu $<, >, \geq, \leq$ vào ô vuông cho thích hợp:

Câu 180 : Đặt dấu $<, >, \geq, \leq$ vào ô vuông cho thích hợp:

Câu 181 : Cho m < n, hãy so sánh: m + 2 và n + 2

Câu 182 : Cho m < n, hãy so sánh: m – 5 và n – 5

Câu 183 : Với m bất kì, hãy chứng tỏ: 1 + m < 2 + m

Câu 184 : Với m bất kì, hãy chứng tỏ: m – 2 < 3 + m

Câu 185 : Với số a bất kì, so sánh: a với a – 1

Câu 186 : Với số a bất kì, so sánh: a với a + 2

Câu 187 : Dùng dấu $<, >, \geq, \leq$ để so sánh m và n nếu: m – n = 2

Câu 188 : Dùng dấu $<, >, \geq, \leq$ để so sánh m và n nếu: m – n = 0

Câu 189 : Dùng dấu $<, >, \geq, \leq$ để so sánh m và n nếu: n – m = 3

Câu 190 : Dựa vào tính chất liên hệ giữa thứ tự và phép cộng, hãy chứng tỏ rằng: Nếu m > n thì m – n > 0

Câu 191 : Dựa vào tính chất liên hệ giữa thứ tự và phép cộng, hãy chứng tỏ rằng: Nếu m – n > 0 thì m > n

Câu 192 : Cho a + 2 > 5, chứng tỏ a > 3. Điều ngược lại là gì? Điều đó có đúng không?

Câu 193 : Khoanh tròn vào chữ cái trước khẳng định đúng trong các khẳng định sau:

Câu 194 : Cho biết a – 7 > b – 7. Khoanh tròn vào trước khẳng định đúng trong các khẳng định sau:

Câu 195 : Đặt dấu $<, >, \geq, \leq$ vào ô vuông cho thích hợp:

Câu 196 : Đặt dấu $<, >, \geq, \leq$ vào ô vuông cho thích hợp:

Câu 197 : Đặt dấu $<, >, \geq, \leq$ vào ô vuông cho thích hợp:

Câu 198 : Đặt dấu $<, >, \geq, \leq$ vào ô vuông cho thích hợp:

Câu 199 : Cho m < n, hãy so sánh: 5m và 5n

Câu 200 : Cho m < n, hãy so sánh: -3m và -3n

Câu 201 : Số b là số âm, số 0 hay số dương nếu: 5b > 3b

Câu 202 : Số b là số âm, số 0 hay số dương nếu: -12b > 8b

Câu 203 : Số b là số âm, số 0 hay số dương nếu: -6b $\geq$ 9b

Câu 204 : Số b là số âm, số 0 hay số dương nếu: 3b $\leq$ 15b

Câu 205 : Cho a < b, hãy đặt dấu <, > vào ô vuông cho thích hợp:

Câu 206 : Cho a < b, hãy đặt dấu <, > vào ô vuông cho thích hợp:

Câu 207 : Cho m > n, chứng tỏ: m + 3 > n + 1

Câu 208 : Cho m > n, chứng tỏ: 3m + 2 > 3n

Câu 209 : Cho m < n, chứng tỏ: 2m + 1 < 2n + 1

Câu 210 : Cho m < n, chứng tỏ: 4(m – 2) < 4(n – 2)

Câu 211 : Cho m < n, chứng tỏ: 3 – 6m > 3 – 6n

Câu 212 : Cho m < n, chứng tỏ: 4m + 1 < 4n + 5

Câu 213 : Cho m < n, chứng tỏ: 3 – 5m > 1 – 5n

Câu 214 : Cho a > 0, b > 0, nếu a < b, hãy chứng tỏ: $a^{2}$ < ab và ab < $b^{2}$

Câu 215 : Cho a > 0, b > 0, nếu a < b, hãy chứng tỏ: $a^{2}$ < $b^{2}$ và $a^{3}$ < $b^{3}$

Câu 216 : Cho a > 5, hãy cho biết bất đẳng thức nào xảy ra: a + 5 > 10

Câu 217 : Cho a > 5, hãy cho biết bất đẳng thức nào xảy ra: a + 4 > 8

Câu 218 : Cho a > 5, hãy cho biết bất đẳng thức nào xảy ra: -5 > -a

Câu 219 : Cho a > 5, hãy cho biết bất đẳng thức nào xảy ra: 3a > 13

Câu 220 : Cho a là số bất kì, hãy đặt dấu $< > \geq \leq$ vào ô vuông cho thích hợp: $a^{2}$ 0

Câu 221 : Cho a là số bất kì, hãy đặt dấu $< > \geq \leq$ vào ô vuông cho thích hợp: - $a^{2}$ 0

Câu 222 : Cho a là số bất kì, hãy đặt dấu $< > \geq \leq$ vào ô vuông cho thích hợp: $a^{2}$ + 1 0

Câu 223 : Cho a là số bất kì, hãy đặt dấu $< > \geq \leq$ vào ô vuông cho thích hợp: – $a^{2}$ – 2 0

Câu 224 : Cho a > b và m < n, hãy đặt dấu >, < vào ô vuông cho thích hợp: a(m – n) b(m – n)

Câu 225 : Cho a > b và m < n, hãy đặt dấu >, < vào ô vuông cho thích hợp: m(a – b) n(a – b)

Câu 226 : Cho 2a > 8, chứng tỏ a > 4. Điều ngược lại là gì? Điều đó có đúng không ?

Câu 227 : Cho bất đẳng thức m > 0. Nhân cả hai vế của bất đẳng thức với số nào thì được bất đẳng thức 1/m > 0?

Câu 228 : Cho bất đẳng thức m < 0. Nhân cả hai vế của bất đẳng thức với số nào thì được bất đẳng thức 1/m < 0?

Câu 229 : Cho a > 0, b > 0 và a > b, chứng tỏ 1a < 1b

Câu 230 : Điền dấu >, < vào ô vuông cho thích hợp: ${(0, 6)}^{2}$ 0,6

Câu 231 : Điền dấu >, < vào ô vuông cho thích hợp: ${(1, 3)}^{2}$ 1,3

Câu 232 : So sánh $m^{2}$ và m nếu: m lớn hơn 1

Câu 233 : So sánh $m^{2}$ và m nếu: m dương nhưng nhỏ hơn 1

Câu 234 : Cho a < b và c < d, chứng tỏ a + c < b + d

Câu 235 : Cho a, b, c, d là các số dương thỏa mãn a < b, c < d, chứng tỏ ac < bd.

Câu 236 : Chứng tỏ rằng với a và b là các số bất kì thì: $a^{2} + b^{2} - 2 a b \geq 0$

Câu 237 : Chứng tỏ rằng với a và b là các số bất kì thì: $(a^{2} + b^{2}) / 2 \geq a b$

Câu 238 : Cho a và b là các số dương, chứng tỏ: $\frac{a}{b} + \frac{b}{a} \geq 2$ .

Câu 239 : Với số a bất kì, chứng tỏ: a(a + 2) < ${(a + 1)}^{2}$

Câu 240 : Chứng minh rằng: Trong ba số nguyên liên tiếp thì bình phương số đứng giữa lớn hơn tích hai số còn lại.

Câu 241 : Cho ba số a, b và k mà a > b. Nếu ak < bk thì số k là

Câu 242 : Cho hai số a và b mà – 7a < -7b

Câu 243 : Cho a là số bất kì, hãy đặt dấu $< > \geq \leq$ vào ô vuông cho đúng |a| 0

Câu 244 : Cho a là số bất kì, hãy đặt dấu $< > \geq \leq$ vào ô vuông cho đúng -|a| 0

Câu 245 : Cho a là số bất kì, hãy đặt dấu $< > \geq \leq$ vào ô vuông cho đúng |a| + 3 0

Câu 246 : Cho a là số bất kì, hãy đặt dấu $< > \geq \leq$ vào ô vuông cho đúng -|a| - 2 0

Câu 247 : Đặt dấu <, > vào ô vuông cho đúng

Câu 248 : Đặt dấu <, > vào ô vuông cho đúng

Câu 249 : Đặt dấu <, > vào ô vuông cho đúng

Câu 250 : Đặt dấu <, > vào ô vuông cho đúng

Câu 251 : Cho x > 0, chứng tỏ: $x + \frac{1}{x} \geq 2$

Câu 252 : Từ kết quả câu a, nếu x < 0 sẽ có kết quả nào ?

Câu 253 : Kiểm tra xem các giá trị sau đây của x có là nghiệm của bất phương trình $x^{2}$ – 2x < 3x . x = 2

Câu 254 : Kiểm tra xem các giá trị sau đây của x có là nghiệm của bất phương trình $x^{2}$ – 2x < 3x . x = 1

Câu 255 : Kiểm tra xem các giá trị sau đây của x có là nghiệm của bất phương trình $x^{2}$ – 2x < 3x . x = -3

Câu 256 : Kiểm tra xem các giá trị sau đây của x có là nghiệm của bất phương trình $x^{2}$ – 2x < 3x . x = 4

Câu 257 : Biểu diễn tập nghiệm của bất phương trình sau trên trục số: x > 5

Câu 258 : Biểu diễn tập nghiệm của bất phương trình sau trên trục số: x < -3

Câu 259 : Biểu diễn tập nghiệm của bất phương trình sau trên trục số: x $\geq$ 4

Câu 260 : Biểu diễn tập nghiệm của bất phương trình sau trên trục số: x $\geq$ -6

Câu 261 : Cho tập A = {-10; -9; -8; -7; -5; -4;……; 8; 9; 10}. Hãy cho biết giá trị nào của x trong tập A sẽ là nghiệm của bất phương trình. |x| < 3

Câu 262 : Cho tập A = {-10; -9; -8; -7; -5; -4;……; 8; 9; 10}. Hãy cho biết giá trị nào của x trong tập A sẽ là nghiệm của bất phương trình. |x| >8

Câu 263 : Cho tập A = {-10; -9; -8; -7; -5; -4;……; 8; 9; 10}. Hãy cho biết giá trị nào của x trong tập A sẽ là nghiệm của bất phương trình. |x| $\leq$ 4

Câu 264 : Cho tập A = {-10; -9; -8; -7; -5; -4;……; 8; 9; 10}. Hãy cho biết giá trị nào của x trong tập A sẽ là nghiệm của bất phương trình. |x| $\geq$ 7

Câu 265 : Hãy đưa ra hai sô nguyên là nghiệm của bất phương trình sau: -4x + 5 > 10

Câu 266 : Hãy đưa ra hai sô nguyên là nghiệm của bất phương trình sau: 2x + 100 < 90

Câu 267 : Viết thành bất phương trình và chỉ ra một nghiệm của nó từ các mệnh đề sau đây: Tổng của số nào đó và 5 lớn hơn 7.

Câu 268 : Viết thành bất phương trình và chỉ ra một nghiệm của nó từ các mệnh đề sau đây: Hiệu của 9 và số nào đó nhỏ hơn -12.

Câu 269 : Viết thành bất phương trình và chỉ ra hai nghiệm của nó từ các mệnh đề sau đây: Tổng của 2 lần số nào đó và 3 lớn hơn 12.

Câu 270 : Viết thành bất phương trình và chỉ ra hai nghiệm của nó từ các mệnh đề sau đây: Hiệu của 5 và 3 lần số nào đó nhỏ hơn 10.

Câu 271 : Cho tập A = {-10; -9; -8; -7;…..; 8; 9; 10}. Hãy cho biết số nào Cho tập A = {-10; -9; -8; -7;…..; 8; 9; 10}. Hãy cho biết số nào là nghiệm của bất phương trình. |x – 2| $\leq$ 3

Câu 272 : Cho tập A = {-10; -9; -8; -7;…..; 8; 9; 10}. Hãy cho biết số nào trong A là nghiệm của bất phương trình. |x – 3| > 5

Câu 273 : Hãy đưa ra ba nghiệm của bất phương trình: 5 > x

Câu 274 : Hãy đưa ra ba nghiệm của bất phương trình: -4 < x

Câu 275 : Viết tập hợp nghiệm của bất phương trình sau bằng kí hiệu tập hợp và biểu diễn tập nghiệm trên trục số. 2 > x

Câu 276 : Viết tập hợp nghiệm của bất phương trình sau bằng kí hiệu tập hợp và biểu diễn tập nghiệm trên trục số. -3 < x

Câu 277 : Khoanh vào chữ cái trước khẳng định đúng.

Câu 278 : Khoanh vào chữ cái trước hình đúng

Câu 279 : Lập bất phương trình cho bài toán sau:

Câu 280 : Áp dụng quy tắc chuyển vế để giải các bất phương trình sau: x – 2 > 4

Câu 281 : Áp dụng quy tắc chuyển vế để giải các bất phương trình sau: x + 5 < 7

Câu 282 : Áp dụng quy tắc chuyển vế để giải các bất phương trình sau: x – 4 < -8

Câu 283 : Áp dụng quy tắc chuyển vế để giải các bất phương trình sau: x + 3 > - 6

Câu 284 : Áp dụng quy tắc chuyển vế, giải các bất phương trình sau: 3x < 2x + 5

Câu 285 : Áp dụng quy tắc chuyển vế, giải các bất phương trình sau: 2x + 1 < x + 4

Câu 286 : Áp dụng quy tắc chuyển vế, giải các bất phương trình sau: -4x – 2 > -5x + 6

Câu 287 : Áp dụng quy tắc nhân để giải các bất phương trình sau: $\frac{1}{2} x > 3$

Câu 288 : Áp dụng quy tắc nhân để giải các bất phương trình sau: $- \frac{1}{3} x < - 2$

Câu 289 : Áp dụng quy tắc nhân để giải các bất phương trình sau: $\frac{2}{3} x > - 4$

Câu 290 : Áp dụng quy tắc nhân để giải các bất phương trình sau: $- \frac{3}{5} x > 6$

Câu 291 : Áp dụng quy tắc nhân, giải các bất phương trình sau: 3x < 18

Câu 292 : Áp dụng quy tắc nhân, giải các bất phương trình sau: -2x > -6

Câu 293 : Áp dụng quy tắc nhân, giải các bất phương trình sau: 0,2x > 8

Câu 294 : Áp dụng quy tắc nhân, giải các bất phương trình sau: -0,3x < 12

Câu 295 : Giải thích sự tương đương: 2x < 3 ⇔ 3x < 4,5

Câu 296 : Giải thích sự tương đương: x – 5 < 12 ⇔ x + 5 < 22

Câu 297 : Giải thích sự tương đương: -3x < 9 ⇔ 6x > -18

Câu 298 : Cho hình vẽ:

Câu 299 : Giải các bất phương trình và biểu diễn tập nghiệm trên trục số 2x – 4 < 0

Câu 300 : Giải các bất phương trình và biểu diễn tập nghiệm trên trục số 3x + 9 > 0

Câu 301 : Giải các bất phương trình và biểu diễn tập nghiệm trên trục số -3x + 12 > 0

Câu 302 : Giải các bất phương trình: 3x + 2 > 8

Câu 303 : Giải các bất phương trình: 4x – 5 < 7

Câu 304 : Giải các bất phương trình: -2x + 1 < 7

Câu 305 : Giải các bất phương trình: 13 – 3x > -2

Câu 306 : Giải các bất phương trình: 3/2 x < -9

Câu 307 : Giải các bất phương trình: 5 + 2/3 x > 3

Câu 308 : Giải các bất phương trình: 2x + 4/5 > 9/5

Câu 309 : Giải các bất phương trình: 6 - 3/5 x < 4

Câu 310 : Giải các bất phương trình: 7x – 2,2 < 0,6

Câu 311 : Giải các bất phương trình: 1,5 > 2,3 – 4x

Câu 312 : Viết bất phương trình bậc nhất một ẩn có tập nghiệm biểu diễn bởi hình vẽ.

Câu 313 : Viết bất phương trình bậc nhất một ẩn có tập nghiệm biểu diễn bởi hình vẽ.

Câu 314 : Giải các bất phương trình: $\frac{3 x - 1}{4} > 2$

Câu 315 : Giải các bất phương trình: $\frac{2 x + 4}{3} < 3$

Câu 316 : Giải các bất phương trình: $\frac{1 - 2 x}{3} > 4$

Câu 317 : Giải các bất phương trình: $\frac{6 - 4 x}{5} < 1$

Câu 318 : Giải các bất phương trình: ${(x - 1)}^{2}$ < x(x + 3)

Câu 319 : Giải các bất phương trình: (x – 2)(x + 2) > x(x – 4)

Câu 320 : Giải các bất phương trình: 2x + 3 < 6 – (3 – 4x)

Câu 321 : Giải các bất phương trình: -2 – 7x > (3 + 2x) – (5 – 6x)

Câu 322 : Với các giá trị nào của x thì: Giá trị phân thức (5 - 2x)/6 lớn hơn giá trị phân thức (5x - 2)/3

Câu 323 : Với các giá trị nào của x thì: Giá trị phân thức (1,5 - x)/5 nhỏ hơn giá trị phân thức (4x + 5)/2

Câu 324 : Hai quy tắc biến đổi tương đương của bất phương trình cũng giống như hai quy tắc biến đổi tương đương của phương trình. Điều đó có đúng không?

Câu 325 : Hãy cho biết số nào trong các số 2/3 ; 2/7 ; -4/5 là nghiệm của bất phương trình 5 – 3x < (4 + 2x) – 1

Câu 326 : Cho bất phương trình ẩn x: 2x + 1 > 2(x + 1). Chứng tỏ các giá trị -5; 0; -8 đều không phải là nghiệm của nó.

Câu 327 : Cho bất phương trình ẩn x: 2x + 1 > 2(x + 1). Bất phương trình này có thể nhận giá trị nào của x là nghiệm?

Câu 328 : Bất phương trình ẩn x: 5 + 5x < 5(x + 2). Có thể nhận giá trị nào của x là nghiệm?

Câu 329 : So sánh số a và số b nếu: x < 5 ⇔ (a – b)x < 5(a – b)

Câu 330 : So sánh số a và số b nếu: x > 2 ⇔ (a – b)x < 2(a – b)

Câu 331 : Tìm số nguyên x lớn nhất thỏa mãn mỗi bất phương trình sau: 5,2 + 0,3x < - 0,5

Câu 332 : Tìm số nguyên x lớn nhất thỏa mãn mỗi bất phương trình sau: 1,2 – (2,1 – 0,2x) < 4,4

Câu 333 : Tìm số nguyên x bé nhất thỏa mãn mỗi bất phương trình sau: 4,2 – (3 – 0,4x) > 0,1x + 0,5

Câu 334 : Tìm số nguyên x bé nhất thỏa mãn mỗi bất phương trình sau: 0,2x + 3,2 > 1,5

Câu 335 : Với giá trị nào của m thì phương trình ẩn x: x – 3 = 2m + 4 có nghiệm dương?

Câu 336 : Với giá trị nào của m thì phương trình ẩn x: 2x – 5 = m + 8 có nghiệm số âm?

Câu 337 : Giải các bất phương trình: ${(x + 2)}^{2}$ < 2x(x + 2) + 4

Câu 338 : Giải các bất phương trình: (x + 2)(x + 4) > (x – 2)(x + 8) + 26

Câu 339 : Giải các bất phương trình: $\frac{1 - 2 x}{4} - 2 < \frac{1 - 5 x}{8}$

Câu 340 : Giải các bất phương trình: $\frac{x - 1}{4} - 1 > \frac{x + 1}{3} + 8$

Câu 341 : Tìm các số tự nhiên n thỏa mãn mỗi bất phương trình sau: 3(5 – 4n) + (27 + 2n) > 0

Câu 342 : Tìm các số tự nhiên n thỏa mãn mỗi bất phương trình sau: ${(n + 2)}^{2}$ – (n – 3)(n + 3) $\leq$ 40

Câu 343 : Khoanh tròn vào chữ cái trước khẳng định đúng.

Câu 344 : Khoanh tròn vào chữ cái trước hình đúng.

Câu 345 : Với giá trị nào của m thì phương trình ẩn x: x – 2 = 3m + 4 có nghiệm lớn hơn 3

Câu 346 : Với giá trị nào của m thì phương trình ẩn x: 3 – 2x = m – 5 có nghiệm nhỏ hơn -2

Câu 347 : Chứng minh hai bất phương trình sau không tương đương 2x + 1 > 3 và |x| > 1

Câu 348 : Chứng minh hai bất phương trình sau không tương đương 3x – 9 < 0 và $x^{2}$ < 9

Câu 349 : Giải các phương trình: |0,5x| = 3 – 2x

Câu 350 : Giải các phương trình: |-2x| = 3x + 4

Câu 351 : Giải các phương trình: |5x| = x – 12

Câu 352 : Giải các phương trình: |-2,5x| = 5 + 1,5x

Câu 353 : Giải các phương trình: |9 + x| = 2x

Câu 354 : Giải các phương trình: |x – 1| = 3x + 2

Câu 355 : Giải các phương trình: |x + 6| = 2x + 9

Câu 356 : Giải các phương trình: |5x| - 3x – 2 = 0

Câu 357 : Giải các phương trình: x – 5x + |-2x| - 3 = 0

Câu 358 : Giải các phương trình: |3 – x| + $x^{2}$ – (4 + x)x = 0

Câu 359 : Giải các phương trình: ${(x - 1)}^{2}$ + |x + 21| - $x^{2}$ – 13 = 0

Câu 360 : Giải các phương trình: |x – 5| = 3

Câu 361 : Giải các phương trình: |x + 6| = 1

Câu 362 : Giải các phương trình: |2x – 5| = 4

Câu 363 : Giải các phương trình: |3x – 2| = 2x

Câu 364 : Giải các phương trình: |2x – 3| = -x + 21

Câu 365 : Với giá trị nào của x thì: |2x – 3| = 2x – 3

Câu 366 : Với giá trị nào của x thì: |5x – 4| = 4 – 5x

Câu 367 : Khoanh tròn vào chữ cái trước khẳng định đúng.

Câu 368 : Khoanh tròn vào chữ cái trước khẳng định đúng.

Câu 369 : Tìm x sao cho |2x − 4| = 6

Câu 370 : Cho các bất đẳng thức:

Câu 371 : Cho a > b, chứng tỏ: 3a + 5 > 3b + 2

Câu 372 : Cho a > b, chứng tỏ: 2 – 4a < 3 – 4b

Câu 373 : Chứng tỏ 2,99 là nghiệm của bất phương trình 3 > x. Hãy kể ra bốn số lớn hơn 2,99 là nghiệm của bất phương trình đó.

Câu 374 : Chứng tỏ 4,01 là nghiệm của bất phương trình 4 < x. Hãy kể ra ba số nhỏ hơn 4,01 là nghiệm của bất phương trình đó.

Câu 375 : Giải các bất phương trình và biểu diễn tập nghiệm của chúng trên trục số. 2(3x – 1) – 2x < 2x + 1

Câu 376 : Giải các bất phương trình và biểu diễn tập nghiệm của chúng trên trục số. 4x – 8 $\geq$ 3(3x – 2) + 4 – 2x

Câu 377 : Giải các bất phương trình: $2 x + 1, 4 < \frac{3 x - 7}{5}$

Câu 378 : Giải các bất phương trình: $1 + \frac{1 + 2 x}{3} > \frac{2 x - 1}{6} - 2$

Câu 379 : Một người đi bộ quãng đường dài 18km trong khoảng thời gian không nhiều hơn 4 giờ. Lúc đầu người đó đi với vận tốc 5km/h, về sau đi với vận tốc 4km/h. Xác định độ dài đoạn đường mà người đó đã đi với vận tốc 5km/h.

Câu 380 : Giải các phương trình: |2x| = 3x – 2

Câu 381 : Giải các phương trình: |x + 15| = 3x – 1

Câu 382 : Chứng tỏ rằng, trong một tam giác độ dài một cạnh luôn nhỏ hơn nửa chu vi.

Câu 383 : Với số m và số n bất kì, chứng tỏ rằng: ${(m + 1)}^{2}$ $\geq$ 4m

Câu 384 : Với số m và số n bất kì, chứng tỏ rằng: $m^{2}$ + $n^{2}$ + 2 $\geq$ 2(m + n)

Câu 385 : Cho a > 0 và b > 0, chứng tỏ rằng: $(a + b) (\frac{1}{a} + \frac{1}{b}) \geq 4$

Câu 386 : Chứng tỏ diện tích của hình vuông có cạnh 10m không nhỏ hơn diện tích hình chữ nhật có cùng chu vi.

Câu 387 : Giải các bất phương trình: 3(x – 2)(x + 2) < 3 $x^{2}$ + x

Câu 388 : Giải các bất phương trình: (x + 4)(5x – 1) > 5 $x^{2}$ + 16x + 2

Câu 389 : Giải các bất phương trình: $\frac{5 x^{2} - 3 x}{5} + \frac{3 x + 1}{4} < \frac{x (2 x + 1)}{2} - \frac{3}{2}$

Câu 390 : Giải các bất phương trình: $\frac{5 x - 20}{3} - \frac{2 x^{2} + x}{2} > \frac{x (1 - 3 x)}{3} - \frac{5 x}{4}$

Câu 391 : Với giá trị nào của x thì:

Câu 392 : Với giá trị nào của x thì:

Câu 393 : Tìm x sao cho: – $x^{2}$ < 0

Câu 394 : Tìm x sao cho: (x – 1)x < 0

Câu 395 : Tìm x sao cho: $x^{2}$ > 0

Câu 396 : Tìm x sao cho: (x – 2)(x – 5) > 0

Câu 397 : Với giá trị nào của x thì: (x - 2)/(x - 3) > 0

Câu 398 : Với giá trị nào của x thì: (x + 2)/(x - 5) < 0

Câu 399 : Chứng tỏ các phương trình sau vô nghiệm: |2x + 3| = 2x + 2

Câu 400 : Chứng tỏ các phương trình sau vô nghiệm: |5x – 3| = 5x – 5

Câu 401 : Tìm x sao cho $\frac{2 x - 1}{x + 3} > 1$

Câu 402 : Tìm x sao cho $\frac{2 x - 1}{x - 2} < 3$

Câu 403 : Viết tỉ số của các cặp đoạn thẳng sau AB = 125cm, CD = 625cm

Câu 404 : Viết tỉ số của các cặp đoạn thẳng sau MN =555cm, M'N'=999cm

Câu 405 : Viết tỉ số của các cặp đoạn thẳng sau EF = 45cm, E'F' = 13,5dm

Câu 406 : Viết tỉ số của các cặp đoạn thẳng sau PQ =10101cm, P'Q' = 303,03m

Câu 407 : Đoạn thẳng AB gấp năm lần đoạn thẳng CD; đoạn thẳng A'B' gấp 7 lần đoạn thẳng CD. Tính tỉ số của hai đoạn thẳng AB và A'B'.

Câu 408 : Đoạn thẳng AB gấp năm lần đoạn thẳng CD; đoạn thẳng A'B' gấp 7 lần đoạn thẳng CD. Cho biết đoạn thẳng MN = 505cm và đoạn M'N' = 707cm, hỏi hai đoạn thẳng AB, A'B' có tỉ lệ với hai đoạn thẳng MN và M'N' hay không?

Câu 409 : Tính độ dài x củạ đoạn thẳng trong hình, biết rằng các số trên hình cùng đơn vị đo cm.

Câu 410 : Cho hình thang ABCD có AB // CD và AB < CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.

Câu 411 : Cho hình thang ABCD có AB // CD và AB < CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.

Câu 412 : Cho hình thang ABCD có AB // CD và AB < CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.

Câu 413 : Cho tam giác ABC. Từ điểm D trên cạnh BC, kẻ các đường thẳng song song với các cạnh AB và AC, chúng cắt các cạnh AC và AB theo thứ tự tại F và E. Chứng minh rằng: $\frac{A E}{A B} + \frac{A F}{A C} = 1$

Câu 414 : Hai đoạn thẳng AB = 35cm, CD = 105cm tỉ lệ với hai đoạn thẳng A'B' = 75cm và C'D'

Câu 415 : Tam giác ABC vuông tại A có đường cao là AD (D ∈ BC). Từ D, kẻ DE vuông góc với AB (E ∈ AB) và DF vuông góc với AC (F ∈ AC).

Câu 416 : Cho tam giác ABC có Cạnh BC = a. Trên cạnh AB lấy các điểm D và E sao cho AD = DE = EB. Từ D, E kẻ các đường thẳng song song với BC, cắt cạnh AC theo thứ tự tại M và N. Tính theo a độ dài các đoạn thẳng DM và EN.

Câu 417 : Cho hình vẽ bên

Câu 418 : Hình vẽ cho biết tam giác ABC vuông tại A, MN // BC, AB = 24cm, AM = 16cm, AN = 12cm. Tính độ dài x, y của các đoạn thẳng NC, BC.

Câu 419 : Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O

Câu 420 : Cho hình thang ABCD (AB // CD). Đường thẳng song song với đáy AB cắt các cạnh bên và các đường chéo AD, BD, AC, và BC theo thứ tự các điểm M, N, P, Q. Chứng minh rằng MN = PQ.

Câu 421 : Cho hình thang ABCD (AB // CD). Trên cạnh AD lấy điểm E sao cho $\frac{A E}{E D} = \frac{p}{q}$ .Qua E kẻ đường thẳng song song với các đáy và cắt BC tại F. Chứng minh rằng: $A E = \frac{p . C D + q . A B}{p + q}$

Câu 422 : Cho hình thang ABCD (AB // CD). Đường thẳng song song với đáy AB cắt các cạnh bên và các đường chéo AD, BD, AC, và BC theo thứ tự các điểm M, N, P, Q. Chứng minh rằng MN = PQ.

Câu 423 : Cho hình thang ABCD (AB // CD). Trên cạnh AD lấy điểm E sao cho $\frac{A E}{E D} = \frac{p}{q}$ .Qua E kẻ đường thẳng song song với các đáy và cắt BC tại F. Chứng minh rằng: $E F = \frac{p . C D + q . A B}{p + q}$

Câu 424 : Hình thang cân ABCD (AB//CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N theo thứ tự là trung điểm của BD và AC. Cho biết MD = 3MO, đáy lớn CD = 5,6cm. Tính độ dài đoạn thẳng MN và đáy nhỏ AB.

Câu 425 : Hình thang cân ABCD (AB//CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N theo thứ tự là trung điểm của BD và AC. Cho biết MD = 3MO, đáy lớn CD = 5,6cm. So sánh độ dài đoạn thẳng MN với nửa hiệu của CD và AB

Câu 426 : Cho hình thang ABCD (AB // CD, AB < CD). Gọi trung điểm các đường chéo AC, BD thứ tự là N và M. Chứng minh rằng: MN // AB

Câu 427 : Cho hình thang ABCD (AB // CD, AB < CD). Gọi trung điểm các đường chéo AC, BD thứ tự là N và M. Chứng minh rằng: MN = (CD-AB)/2

Câu 428 : Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M, N. Chứng minh rằng OM = ON.

Câu 429 : Cho trước ba đoạn thẳng có độ dài tương ứng là m, n, p. Hãy dựng đoạn thẳng thứ tư có độ dài là q sao cho $\frac{m}{n} = \frac{p}{q}$

Câu 430 : Cho đoạn thẳng AB = 3cm, CD = 5cm, EF = 2cm. Hãy đựng đoạn thẳng thứ tự có độ dài là a sao cho $\frac{A B}{C D} = \frac{E F}{a} h a y \frac{3}{5} = \frac{2}{a}$ Tính giá trị của a

Câu 431 : Hình bs.1 cho biết AB // CD, O ∈ MN, MN = 5cm, OB = 1,5cm, OD = 4,5cm, MB = 1cm.

Câu 432 : Hình bs.1 cho biết AB // CD, O ∈ MN, MN = 5cm, OB = 1,5cm, OD = 4,5cm, MB = 1cm.

Câu 433 : Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại O. Chứng minh rằng OM.OC = ON.OB

Câu 434 : Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, K, N, H lần lượt là chân đường vuông góc hạ từ O xuống các cạnh AB, BC, CD, DA. Chứng minh rằng: $\frac{O M}{O N} = \frac{A B}{C D}$

Câu 435 : Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, K, N, H lần lượt là chân đường vuông góc hạ từ O xuống các cạnh AB, BC, CD, DA. Chứng minh rằng: $\frac{O H}{O K} = \frac{B C}{A D}$

Câu 436 : Tam giác ABC có AB = 15cm, AC = 20cm, BC = 25cm. Đường phân giác góc BAC cắt cạnh BC tại D. Tính độ dài các đoạn thẳng DB và DC.

Câu 437 : Tam giác ABC có AB = 15cm, AC = 20cm, BC = 25cm. Đường phân giác góc BAC cắt c ạnh BC tại D.Tính tỉ số diện tích của hai tam giác ABD và ACD.

Câu 438 : Tam giác ABC có các đường phân giác AD,BE,CF

Câu 439 : Tam giác cân ABC có BA = BC = a, AC = b.Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N. Chứng minh MN // AC

Câu 440 : Tam giác cân ABC có BA = BC = a, AC = b.Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N. Tính MN theo a, b.

Câu 441 : Tam giác ABC có AB= 12cm, AC = 20cm, BC= 28cm. Đường phân giác góc A cắt BC tại D. Qua D kẻ DE // AB (E ∈ AC). Tính độ dài các đoạn thẳng BD, DC, DE.

Câu 442 : Tam giác ABC có AB= 12cm, AC = 20cm, BC= 28cm. Đường phân giác góc A cắt BC tại D. Qua D kẻ DE // AB (E ∈ AC). Cho biết diện tích tam giác ABC là S,tính diện tích các tam ABD, ADE, DCE

Câu 443 : Cho tam giác ABC vuông tại A, AB = 21cm, AC = 28cm; đường phân giác góc A cắt BC tại D, đường thắng qua D song song với AB cắt AC tại E. Tính độ dài các đoạn thẳng BD,DC và DE.

Câu 444 : Cho tam giác ABC vuông tại A, AB = 21cm, AC = 28cm; đường phân giác góc A cắt BC tại D, đường thắng qua D song song với AB cắt AC tại E. Tính diện tích tam giác ABD và diện tich tam giác ACD.

Câu 445 : Cho tam giác cân ABC (AB = AC), đường phân giác góc B cắt AC tại D và cho biết AB = 15cm, BC = 10cm.Tính AD, DC.

Câu 446 : Cho tam giác cân ABC (AB = AC), đường phân giác góc B cắt AC tại D và cho biết AB = 15cm, BC = 10cm.Đường vuông góc với BD tại B cắt đường thẳng AC tại E. Tính EC.

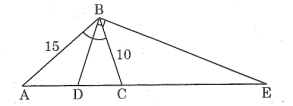
Câu 447 : Tam giác ABC có góc A = $90^{0}$ , AB = 12cm, AC=16cm; đường phân giác góc A cắt BC tại D. Tính BC, BD và DC.

Câu 448 : Tam giác ABC có góc A = $90^{0}$ , AB = 12cm, AC=16cm; đường phân giác góc A cắt BC tại D. Kẻ đường cao AH, tính AH, HD và AD.

Câu 449 : Tam giác ABC có $∠$ A = $90^{0}$ , AB = a (cm), AC = b (cm) (a < b), trung tuyến AM, đường phân giác AD (M và D thuộc cạnh BC). Tính độ dài các đoạn thẳng BC, BD, DC, AM và DM theo a, b

Câu 450 : Tam giác ABC có $∠$ A = $90^{0}$ , AB = a (cm), AC = b (cm) (a < b), trung tuyến AM, đường phân giác AD (M và D thuộc cạnh BC). Hãy tính độ dài các đoạn thẳng trên chính xác đên chữ số thập phân thứ hai khi biết a = 4,15cm, b = 7,25cm.

Câu 451 : Tam giác ABC vuông tại A có đường phân giác AD. Biết rằng độ dài của các cạnh góc vuông AB = 3,75cm, AC = 4,5cm

Câu 452 : Tam giác ABC vuông tại A có đường phân giác AD. Biết rằng độ dài của các cạnh góc vuông AB = 3,75cm, AC = 4,5cm

Câu 453 : Hình bình hành ABCD có độ dài cạnh AB = a = 12,5cm, BC = b = 7,25cm. Đường phân giác của góc B cắt đường chéo AC tại E, đường phân giác của góc D cắt đường chéo AC tại F

Câu 454 : Cho hai tam giác A'B'C' và ABC đồng dạng với nhau theo tỉ số k. Chứng minh rằng tỉ số hai chu vi tam giác cũng bằng k.

Câu 455 : Tam giác ABC có AB = 3cm, BC = 5cm, CA= 7cm. Tam giác A'B'C' đồng dạng với tam giác ABC có cạnh nhỏ nhất là 4,5cm.Tính các cạnh còn lại của tam giác A'B'C'.

Câu 456 : Cho tam giác ABC có AB = 16,2cm, BC = 24,3cm, AC = 32,7cm. Tính độ dài các cạnh của tam giác A'B'C', biết rằng tam giác A'B'C đồng dạng với tam giác ABC và: A'B' lớn hơn cạnh AB là 10,8cm.

Câu 457 : Cho tam giác ABC có AB = 16,2cm, BC = 24,3cm, AC = 32,7cm. Tính độ dài các cạnh của tam giác A'B'C', biết rằng tam giác A'B'C đồng dạng với tam giác ABC và: A'B' bé hơn cạnh AB là 5,4cm.

Câu 458 : Hình thang ABCD (AB // CD) có CD= 2AB. Gọi E là trung điểm của CD. Chứng minh rằng ba tam giác ADE, ABE và BEC đồng dạng với nhau từng đôi một.

Câu 459 : Tam giác ABC có tổng độ dài hai cạnh AB + AC = 10,75 cm và đồng dạng với tam giác A’B’C’ có độ dài các cạnh A’B’ = 8,5cm, A’C’ = 7,35cm, B’C’ = 6,25cm.

Câu 460 : Hai tam giác mà các cạnh có độ dài như sau có đồng dạng không? 4cm; 5cm; 6cm và 8mm; 10mm; 12mm.

Câu 461 : Hai tam giác mà các cạnh có độ dài như sau có đồng dạng không? 3cm; 4cm; 6cm và 9cm; 15cm; 18cm.

Câu 462 : Hai tam giác mà các cạnh có độ dài như sau có đồng dạng không? 1dm; 2dm; 2dm và 1dm; 1dm; 0,5dm

Câu 463 : Tam giác vuông ABC ( $∠ A = 90^{0}$ ) có AB = 6cm, AC = 8cm và tam giác vuông A’B’C’ ( $∠ A' = 90^{0}$ ) có A’B’ = 9cm, B’C’ = 15cm. Hỏi rằng hai tam giác vuông ABC và A’B’C’ có đồng dạng với nhau không? Vì sao?

Câu 464 : Tam giác ABC có ba đường trung tuyến cắt nhau tại O. Gọi P,Q, R theo thứ tự là trung điểm của các đoạn thẳng OA, OB, OC. Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC

Câu 465 : Tam giác ABC có ba góc nhọn và có trực tâm là điểm H. Gọi K, M, N thứ tự là trung điểm của các đoạn thẳng AH, BH, CH.Chứng minh rằng tam giác KMN đồng dạng với tam giác ABC với tỉ số đồng dạng k = 1/2

Câu 466 : Cho tam giác ABC và điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC.

Câu 467 : Cho tam giác ABC và điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Tính chu vi của tam giác PQR, biết rằng tam giác ABC có chu vi p bằng 543 cm.

Câu 468 : Cho tam giác ABC. Hãy dựng một tam giác đồng dạng với tam giác ABC theo tỉ số k =2/3

Câu 469 : Hai tam giác mà các cạnh có độ dài sau đây thì đồng dạng với nhau. Trường hợp nào đúng ? Trường hợp nào sai ? hãy đánh dấu gạch chéo vào ô trả lời thích hợp ở bảng sau:

Câu 470 : Cho tam giác ba góc nhọn ABC và một điểm O bất kì trong tam giác đó.

Câu 471 : Cho tam giác ba góc nhọn ABC và một điểm O bất kì trong tam giác đó.

Câu 472 : Cho tam giác ABC có AB = 12cm, AC = 15cm, BC = 18cm. Trên cạnh AB đặt đoạn thẳng AM = 10cm, trên cạnh AC đặt đoạn AN = 8cm. Tính độ dài đoạn thẳng MN

Câu 473 : Hình thang ABCD (AB // CD) có AB= 4cm, CD = 16cm và BD = 8cm. Chứng minh: $∠$ (BAD) = $∠$ (DBC) và BC =2AD.

Câu 474 : Cho tam giác ABC có $∠$ A = $60^{0}$ ; AB = 6cm, AC = 9cm. Dựng tam giác đồng dạng với tam giác ABC theo tỉ số đồng dạng k = 1/3

Câu 475 : Cho tam giác ABC có $∠$ A = $60^{0}$ ; AB = 6cm, AC = 9cm. Hãy nêu một vài cách dựng khác và vẽ hình từng trường hợp.

Câu 476 : Cho tam giác ABC có AB = 10cm, AC=20cm. Trên cạnh AC, đặt đoạn AD = 5cm. Chứng minh: $∠$ (ABD) = $∠$ (ACB)

Câu 477 : Hình bs.4 cho biết Oz là phân giác của góc xOy, OA = 9cm, OB = 12cm, OC = 16cm, AB = 6cm.

Câu 478 : Hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O và AC = 2.AB. Vẽ trung tuyến BE của tam giác ABO. Chứng minh rằng $∠$ ABE = $∠$ ACB.

Câu 479 : Hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O và AC = 2.AB. Gọi M là trung điểm của cạnh BC, chứng minh rằng EM vuông góc với đường chéo BD.

Câu 480 : Cho hình bình hành ABCD .Gọi E là trung điểm của AB, F là trung điểm của CD. Chứng minh hai tam giác ADE và CBF đồng dạng với nhau.

Câu 481 : Tam giác vuông ABC có $∠ A = 90^{0}$ và đường cao AH. Từ H hạ HK vuông góc vói AC. Trong hình đã cho có bao nhiêu tam giác đồng dạng với nhau?

Câu 482 : Tam giác vuông ABC có $∠ A = 90^{0}$ và đường cao AH. Từ H hạ HK vuông góc vói AC. Hãy viết các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng.

Câu 483 : Hình thang ABCD (AB // CD) có AB =2,5cm, AD = 3,5cm, BD=5cm và $∠$ (DAB) = $∠$ (DBC). Chứng minh tam giác ADB đồng dạng với tam giác BCD.

Câu 484 : Hình thang ABCD (AB // CD) có AB =2,5cm, AD = 3,5cm, BD=5cm và $∠$ (DAB) = $∠$ (DBC). Tính độ dài BC, CD.

Câu 485 : Hình thang ABCD (AB // CD) có AB =2,5cm, AD = 3,5cm, BD=5cm và $∠$ (DAB) = $∠$ (DBC). Sau khi tính, hãy vẽ lại hình chính xác bằng thước và compa.

Câu 486 : Cho tam giác ABC vuông tại A, AC = 9cm, BC = 24cm. Đường trung trực của BC cắt đường thẳng AC tại D, cắt BC tại M. Tính độ dài của đoạn thẳng CD.

Câu 487 : Cho hình thang vuông ABCD ( $∠$ A = $∠$ D = $90^{0}$ ) AB = 6cm, CD = 12cm, AD = 17cm. Trên cạnh AD, đặt đoạn AE = 8cm. Chứng minh $∠$ (BEC) = $90^{0}$

Câu 488 : Cho tam giác ABC vuông tại A, AC =4cm, BC = 6cm. Kẻ tia Cx vuông góc với BC (tia Cx và điểm A khác phía so với đường thẳng BC). Lấy trên Cx điểm D sao cho BD =9cm. Chứng minh rằng BD // AC

Câu 489 : Trên hình vẽ hãy chỉ ra các tam giác đồng dạng .Viết các cặp tam giác đồng dạng theo thứ tự các đỉnh tương ứng và giải thích vì sao chúng đồng dạng

Câu 490 : Cho tam giác ABC ( $∠$ A = $90^{0}$ ) có đường cao AH. Chứng minh rằng $A H^{2} = B H . C H$

Câu 491 : Đường cao của một tam giác vuông xuất phát từ đỉnh góc vuông chia cạnh huyền thành hai đoạn thẳng có dộ dài là 9cm và 16cm; Tính độ dài các cạnh của tam giác vuông.

Câu 492 : Tam giác vuông ABC (A = $90^{0}$ ) có đường cao AH và trung tuyến AM. Tính diện tích tam giác AMH,biết rằng BH = 4cm, CH = 9cm

Câu 493 : Cho góc nhọn xOy.

Câu 494 : Tam giác ABC vuông tại A có đường cao AH = n = 10,85cm và cạnh AB = m = 12,5cm. Hãy tính độ dài các cạnh còn lại của tam giác (chính xác đến hai chữ số thập phân)

Câu 495 : Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn có độ dài 4cm và 9cm.

Câu 496 : Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn có độ dài 4cm và 9cm.

Câu 497 : Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn có độ dài 4cm và 9cm.

Câu 498 : Cho tam giác ABC. Trên cạnh AB lấy điểm M sao cho $\frac{A M}{M B} = \frac{2}{3}$ tìm trên AC điểm N sao cho $\frac{A N}{N C} = \frac{2}{3}$

Câu 499 : Cho tam giác ABC. Vẽ đoạn thẳng MN. Hỏi rằng hai đường thẳng MN và BC có song song với nhau không? Vì sao?

Câu 500 : Cho tam giác ABC. Cho biết chu vi và diện tích của tam giác ABC thứ tư là P và S. Tính chu vi và diện tích tam giác AMN.

Câu 501 : Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O, $∠$ (BAO) = $∠$ (BDC) .Chứng minh: $△$ ABO đồng dạng $△$ DCO

Câu 502 : Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O, $∠$ (BAO) = $∠$ (BDC) .Chứng minh: $△$ BCO đồng dạng $△$ ADO

Câu 503 : Cho hình chữ nhật ABCD có AB = a = 12cm, BC = b = 9m. Gọi H là chân đường vuông góc kẻ từ A xuống BD. Chứng minh $△$ AHB đồng dạng $△$ BCD

Câu 504 : Cho hình chữ nhật ABCD có AB = a = 12cm, BC = b = 9m. Gọi H là chân đường vuông góc kẻ từ A xuống BD. Tính độ dài đoạn thẳng AH

Câu 505 : Cho hình chữ nhật ABCD có AB = a = 12cm, BC = b = 9m. Gọi H là chân đường vuông góc kẻ từ A xuống BD. Tính diện tích tam giác AHB.

Câu 506 : Tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O, $∠$ (ABD) = $∠$ (ACD) . Gọi E là giao điểm của hai đường thẳng AD và BC. Chứng minh rằng: $△$ AOB đồng dạng $△$ DOC

Câu 507 : Tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O, $∠$ (ABD) = $∠$ (ACD) . Gọi E là giao điểm của hai đường thẳng AD và BC. Chứng minh rằng: $△$ ẠOD đồng dạng $△$ BOC

Câu 508 : Tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O, $∠$ (ABD) = $∠$ (ACD) . Gọi E là giao điểm của hai đường thẳng AD và BC. Chứng minh rằng: EA.ED = EB.EC.

Câu 509 : Tam giác ABC có ba đường cao AD, BE, CF đồng quy tại H.Chứng minh rằng:AH.DH = BH.EH = CH.FH

Câu 510 : Hai điểm M và K thứ tự nằm trên cạnh AB và BC của tam giác ABC; hai đoạn thẳng AK và CM cắt nhau tại P. Biết AP = 2PK và CP = 2PM. Chứng minh rằng AK và CM là các trung tuyến của tam giác ABC

Câu 511 : Cho hình bình hành ABCD .Từ A kẻ AM vuông góc với BC,AN vuông góc CD (M thuộc BC và N thuộc CD). Chứng mình rằng tam giác MAN đồng dạng với tam giác ABC.

Câu 512 : Giả sử AC là đường chéo lớn của hình bình hành ABCD. Từ C, vẽ đường thẳng vuông góc CE với đường thẳng AB, đường vuông góc CF với đường thẳng AD (E, F thuộc phần kéo dài của các cạnh AB và AD), Chứng minh rằng AB.AE + AD.AF = $A C^{2}$

Câu 513 : Tam giác ABC có hai đường cao là AD và BE (D thuộc BC và E thuộc AC). Chứng minh hai tam giác DEC và ABC là hai tam giác đồng dạng.

Câu 514 : Tam giác ABC có hai đường trung tuyến AK và CL cắt nhau tại O. Từ điểm P bất kì trên cạnh AC, vẽ các đường thẳng PE song song với AK, PF song song với CL (E thuộc BC, F thuộc AB).Các trung tuyến AK, CL cắt đoạn thẳng EF theo thứ tự tại M, N. Chứng minh rằng các đoạn thẳng FM, MN, NE bằng nhau

Câu 515 : Điền thêm vào chỗ trống(…) Tên gọi của hình vẽ….

Câu 516 : Điền thêm vào chỗ trống(…) Hình này có …..cạnh

Câu 517 : Điền thêm vào chỗ trống(…) Hình này có …..mặt

Câu 518 : Điền thêm vào chỗ trống(…) Hình này có …. đỉnh

Câu 519 : Xem hình vẽ hãy: Gọi tên các mặt phẳng chứa đường thắng PR.

Câu 520 : Xem hình vẽ hãy: Gọi tên các mặt phẳng chứa đường thẳng PR nhưng chưa thấy rõ trên hình vẽ

Câu 521 : Xem hình vẽ hãy: Gọi tên mặt phẳng cũng chứa các đường thẳng PQ và MV.

Câu 522 : $A B C D . A_{1} B_{1} C_{1} D_{1}$ là một hình hộp chữ nhật. Nếu 0 là trung điểm của đoạn AB thì 0 có là trung điểm của đoạn $A B_{1}$ hay không?

Câu 523 : $A B C D . A_{1} B_{1} C_{1} D_{1}$ là một hình hộp chữ nhật. K thuộc cạnh BC; liệu K có thể là điểm thuộc cạnh $D D_{1}$ hay không?

Câu 524 : Cho hình hộp chữ nhật $A B C D . A_{1} B_{1} C_{1} D_{1}$ . Vẽ một đường chéo của mặt ( $D C C_{1} D_{1}$ ). Liệu đường chéo này có cắt các đường thẳng $C D . D_{1} C, D D_{1}$ hay không?

Câu 525 : Quan sát hình vẽ và điền Đ(đúng) hoặc S(sai) và ô vuông

Câu 526 : Chọn kết quả đúng trong các phát biểu dưới đây:

Câu 527 : Tìm trên hình hộp chữ nhật $A B C D . A_{1} B_{1} C_{1} D_{1}$ một ví dụ để chứng tỏ các mệnh để sau đây là sai

Câu 528 : Tìm trên hình hộp chữ nhật $A B C D . A_{1} B_{1} C_{1} D_{1}$ một ví dụ để chứng tỏ các mệnh để sau đây là sai

Câu 529 : Quan sát hình hộp chữ nhật. Các cặp mặt phẳng nào song song với nhau?

Câu 530 : Quan sát hình hộp chữ nhật. Các điểm D, H, G và C có cùng thuộc một mặt phẳng hay không?

Câu 531 : Quan sát hình hộp chữ nhật. Các diểm D, H, G và F có cùng thuộc một mặt phẳng hay không?

Câu 532 : Quan sát hình hộp chữ nhật. Câu hỏi tương tự như b, c đối với các điểm A, B, G và H.

Câu 533 : Tìm diện tích toàn phần của hình hộp chữ nhật theo các kích thước cho ở hình vẽ.

Câu 534 : $A B C D . A_{1} B_{1} C_{1} D_{1}$ là một hình lập phương. Khi nối A với $C_{1}$ và B với $D_{1}$ thì hai đường thẳng $A C_{1}$ và $B D_{1}$ có cắt nhau hay không?

Câu 535 : $A B C D . A_{1} B_{1} C_{1} D_{1}$ là một hình lập phương. $A C_{1}$ và $A_{1} C$ có cắt nhau hay không?

Câu 536 : $A B C D . A_{1} B_{1} C_{1} D_{1}$ là một hình lập phương. Câu hỏi tương tự như câu b với $B D_{1}$ và. $A_{1} A$

Câu 537 : Quan sát hình lập phương $A B C D . A_{1} B_{1} C_{1} D_{1}$

Câu 538 : Quan sát hình lập phương $A B C D . A_{1} B_{1} C_{1} D_{1}$

Câu 539 : Tìm trong hình hộp chữ nhật $A B C D . A_{1} B_{1} C_{1} D_{1}$ một ví dụ cụ thể để chứng tỏ phát biểu sau đây là sai. Hai đường thẳng nằm trong hai mặt phẳng song song thì song song với nhau.

Câu 540 : Khi gấp và dán hình những dưới đây ,hình nào tạo thành hình lập phương

Câu 541 : Tìm số hình lập phương đơn vị (hình lập phương có cạnh là 1) ở các hình

Câu 542 : Tìm số hình lập phương đơn vị (hình lập phương có cạnh là 1) ở các hình

Câu 543 : Từ một đoạn dây thép ngắn hơn 1,5m liệu người ta tạo ra một hình lập phương có cạnh là 1dm được hay không? (đoạn dây thép để nguyên không cắt).

Câu 544 : Quan sát hình hộp chữ nhật và trả lời các câu hỏi sau: Ba đường nào cắt nhau tại G?

Câu 545 : Quan sát hình hộp chữ nhật và trả lời các câu hỏi sau: Hai mặt phẳng nào cắt nhau theo đường thẳng FB?

Câu 546 : Quan sát hình hộp chữ nhật và trả lời các câu hỏi sau: Mặt phẳng (EFBA) và mặt phẳng (FGCB) cắt nhau theo đường thẳng nào?

Câu 547 : Cạnh hình lập phương bằng $\sqrt{2}$ . Như vậy độ dài đoạn $A C_{1}$ là :

Câu 548 : Một hình hộp chữ nhật có các kích thước như hình vẽ. Để xếp kín hình hộp đã cho bằng các hình hộp chữ nhật có các kích thước dài 8cm, rộng 6cm, cao 4cm thì số hình hộp cần phải có là:

Câu 549 : Hãy giải thích vì sao để cột thẳng đứng hoặc khi làm đế của chân bàn, người ta lại neo cái cọc, đóng mộng chân bàn.

Câu 550 : Từ một tấm giấy hình vuông kích thước 3 x 3 liệu có thể ghép thành một hình lập phương đơn vị hay không? (có thể làm nắp rời).

Câu 551 : Tìm trên hình hộp chữ nhật $A B C D . A_{1} B_{1} C_{1} D_{1}$ một ví dụ cụ thể để chứng tỏ mệnh để sau đây là sai: Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau

Câu 552 : Các kích thước của một hình hộp chữ nhật như hình vẽ, độ dài đoạn $A C_{1}$ là:

Câu 553 : Quan sát hình vẽ và điền vào chỗ trống kết quả bằng số:

Câu 554 : Quan sát hình vẽ và điền vào chỗ trống kết quả bằng số:

Câu 555 : Trong các hình dưới đây, mỗi hình có bao nhiêu đơn vị diện tích và bao nhiêu đơn vị thể tích (mỗi hình nhỏ là một hình lập phương đơn vị).

Câu 556 : Trong các hình dưới đây, mỗi hình có bao nhiêu đơn vị diện tích và bao nhiêu đơn vị thể tích (mỗi hình nhỏ là một hình lập phương đơn vị).

Câu 557 : Trong các hình dưới đây, mỗi hình có bao nhiêu đơn vị diện tích và bao nhiêu đơn vị thể tích (mỗi hình nhỏ là một hình lập phương đơn vị).

Câu 558 : Trong các hình dưới đây, mỗi hình có bao nhiêu đơn vị diện tích và bao nhiêu đơn vị thể tích (mỗi hình nhỏ là một hình lập phương đơn vị).

Câu 559 : Cho các hình lăng trụ đứng với kích thước như các hình dưới.

Câu 560 : Cho các hình lăng trụ đứng với kích thước như các hình dưới.

Câu 561 : Cho các hình lăng trụ đứng với kích thước như các hình dưới.

Câu 562 : Trong các hình vẽ sau đây, hình vẽ nào biểu diễn một hình lăng trụ đứng?

Câu 563 : Một lăng trụ đứng, đáy là một tam giác thì lăng trụ đó có:

Câu 564 : Hãy cho bịết: Một lăng trụ đứng có 6 mặt thì đáy của hình lăng trụ là hình gì?

Câu 565 : Hãy cho bịết: Một lăng trụ đứng có 8 mặt thì đáy của hình lăng trụ là hình gì?

Câu 566 : Hình vẽ biểu diễn một lăng trụ đứng có đáy là tam giác. Trong các phát biểu sau, phát biểu nào là đúng?

Câu 567 : ABCD.XYHK là một lăng trụ đứng có đáy là một hình chữ nhật. Quan sát hình và chỉ ra những cặp mặt phẳng song song với nhau.

Câu 568 : ABCD.XYHK là một lăng trụ đứng có đáy là một hình chữ nhật. Những cặp mặt phẳrig nào vuông góc với nhau?

Câu 569 : ABCD.XYHK là một lăng trụ đứng có đáy là một hình chữ nhật. Sử dụng kí hiệu // và ⊥ để điền vào các ô trống ở bảng sau:

Câu 570 : ABCD.XYHK là một lăng trụ đứng có đáy là một hình chữ nhật. Sử dụng kí hiệu // và ⊥ để điền vào các ô trống ở bảng sau:

Câu 571 : Quan sát các hình khai triển trên hình vẽ dưới rồi cho biết: Cạnh nào sẽ được ghép với cạnh AB để được hình lăng trụ đứng (sử dụng các số cho trên hình)

Câu 572 : Quan sát các hình khai triển trên hình vẽ dưới rồi cho biết: Cạnh nào sẽ được ghép với cạnh AB để được hình lăng trụ đứng (sử dụng các số cho trên hình)

Câu 573 : Quan sát các hình lăng trụ đứng trên hình vẽ rồi điền số thích hợp vào các ô trống ở bảng sau:

Câu 574 : Quan sát các hình lăng trụ đứng trên hình vẽ rồi điền số thích hợp vào các ô trống ở bảng sau:

Câu 575 : Quan sát các hình lăng trụ đứng trên hình vẽ rồi điền số thích hợp vào các ô trống ở bảng sau:

Câu 576 : Diện tích toàn phần của cái tủ âm tường hình lăng trụ đứng như hình vẽ là bao nhiêu?

Câu 577 : Người ta cắt một khối gỗ có dạng một hình lập phương như hình vẽ (cắt theo mặt $A C C_{1} A_{1}$ ) và được hai lăng trụ đứng. Đáy lăng trụ đứng nhận được là tam giác vuông, tam giác cân, hay là tam giác đều?

Câu 578 : Người ta cắt một khối gỗ có dạng một hình lập phương như hình vẽ (cắt theo mặt $A C C_{1} A_{1}$ ) và được hai lăng trụ đứng. Các mặt bên của mỗi lăng trụ đứng nhận được có phải tất cả đều là hình vuông hay không

Câu 579 : Vẽ hình khai triển (cắt theo các cạnh $B_{1} C_{1}$ , $C B_{1}$ , $C_{1} A_{1}$ ,CA) của lăng trụ đứng đáy tam giác có các kích thước cho như hình bên với a = 5cm, c = 4,2cm, hc = 4cm, h = 3,8cm

Câu 580 : Một cái chân giấy bằng thủy tinh hình lăng trụ đứng có kích thước như hình vẽ .Diện tích toàn phần của nó là:

Câu 581 : Đáy của lăng trụ đúng là một hình thang cân có các cạnh b =11mm, a = 15mm và chiều cao hr =7mm.Chiều cao lăng trụ đứng là h=14mm.Tính diện tích xung quanh hình lăng trụ

Câu 582 : Cho hình hộp chủ nhật $D E_{1} B G_{1} H F_{1} E G$ có dạng như hình vẽ..

Câu 583 : Một lăng trụ đứng lục giác đều có độ dài cạnh đáy là 6cm, chiều cao của lăng trụ là 10cm. Diện tích toàn phần của lăng trụ đó là (đơn vị $c m^{2}$ )

Câu 584 : Hình bên là một cái lều ở trại hè, có dạng một lăng trụ đứng kèm theo kích thước. Sau đây là ba kiểu mà học sinh lựa chọn.

Câu 585 : Hình bên là một cái lều ở trại hè, có dạng một lăng trụ đứng kèm theo kích thước. Sau đây là ba kiểu mà học sinh lựa chọn.

Câu 586 : Hình bên là một cái lều ở trại hè, có dạng một lăng trụ đứng kèm theo kích thước. Sau đây là ba kiểu mà học sinh lựa chọn.

Câu 587 : Tìm diện tích toàn phần của hình lăng trụ đứng theo các kích thước cho trên hình.

Câu 588 : Diện tích toàn phần của hình lăng trụ đứng tính theo kích thước trên hình là:

Câu 589 : Quan sát hình lăng trụ đứng. Các phát biểu sau đây đúng hay sai?

Câu 590 : Thể tích hình lăng trụ đứng theo các kích thước trên hình là:

Câu 591 : Tính giá trị của x theo các kích thước cho trên hình, biết thể tích lăng trụ đứng bằng 15 $c m^{3}$

Câu 592 : Tính thể tích theo các kich thước đã cho của các hình lăng trụ sau đây.

Câu 593 : Tính thể tích theo các kich thước đã cho của các hình lăng trụ sau đây.

Câu 594 : Tính thể tích phần không gian của một ngôi nhà dạng một lăng trụ đứng theo các kích thước đã cho trong hình.

Câu 595 : Lăng trụ đứng có kích thước như hình vẽ có thể tích là:

Câu 596 : Theo các kích thước của hình lăng trụ đứng đáy tam giác cho trên hình thì trong các số sau:

Câu 597 : Một nhà kho có dạng lăng trụ đứng như hình vẽ với BC = ED = CD = 10m và DH = 20m, AB = AE Chiều cao từ đỉnh A đến nền nhà là 15m. Thể tích của kho là ( $m^{3}$ )

Câu 598 : Tính thể tích và diện tích toàn phần của các hình lăng trụ đứng có các kích thước cho trong hình vẽ

Câu 599 : Tính thể tích và diện tích toàn phần của các hình lăng trụ đứng có các kích thước cho trong hình vẽ

Câu 600 : Đố : ta có một cái khay hình hộp chữ nhật ,dùng nó để lấy nước pha một dung dịch .Không sử dụng các dụng cụ đo,có thể đong được một lượng nước bằng mấy phần của khay? (không đánh dấu vào khay)

Câu 601 : Thể tích hình lăng trụ đứng theo các kích thước trên hình là:

Câu 602 : Thể tích hình lăng trụ đứng được cho theo các kích thước ở hình là:

Câu 603 : Hãy tính thể tích các hình dưới đây theo các kích thước cho trên hình vẽ

Câu 604 : Hãy tính thể tích các hình dưới đây theo các kích thước cho trên hình vẽ

Câu 605 : Hãy tính thể tích các hình dưới đây theo các kích thước cho trên hình vẽ

Câu 606 : Hãy tính thể tích các hình dưới đây theo các kích thước cho trên hình vẽ

Câu 607 : Hãy tính thể tích các hình dưới đây theo các kích thước cho trên hình vẽ

Câu 608 : Hãy tính thể tích các hình dưới đây theo các kích thước cho trên hình vẽ

Câu 609 : Hãy tính thể tích các hình dưới đây theo các kích thước cho trên hình vẽ

Câu 610 : Hình chóp tứ giác đều S.ABCD có các mặt bên là những tam giác đều AB =8cm,O là trung điểm của AC.Độ dài đoạn SO là:

Câu 611 : Hình chóp lục giác đều S.ABCDEH có AB = 6cm, cạnh bên SA = 10 cm.

Câu 612 : Tính diện tích toàn phần của hình chóp tam giác đều theo các kích thước trên hình vẽ.

Câu 613 : Cho hình chóp tứ giác đều. Điền số thích hợp vào ô còn lại trong bảng sau:

Câu 614 : Một hình chóp tứ giác đều có độ dài cạnh đáy là = 6cm, chiều cao là 4cm thì diện tích xung quanh là:

Câu 615 : Hình chóp đều S.ABC có cạnh đáy bằng a=12cm,chiều cao h=8cm.Hãy tính diện tích xung quanh của hình chóp đó

Câu 616 : Một hình chóp tứ giác đều và một lăng trụ đứng tứ giác đều như hình vẽ .Nếu thể tích hình trụ là V thì thể tích hình chóp là:

Câu 617 : Một cái nhà trồng cây thí nghiệm có dạng hình lăng trụ đứng có các kích thước như hình vẽ trong đó EDC là tam giác cân.Hãy tính : Diện tích hình ABCDE

Câu 618 : Một cái nhà trồng cây thí nghiệm có dạng hình lăng trụ đứng có các kích thước như hình vẽ trong đó EDC là tam giác cân.Hãy tính : Tính thể tích nhà kính

Câu 619 : Một cái nhà trồng cây thí nghiệm có dạng hình lăng trụ đứng có các kích thước như hình vẽ trong đó EDC là tam giác cân.Hãy tính : Diện tích kính cần phải có để “lợp” hai mái và bốn bức tường nhà

Câu 620 : Hình vẽ là chiếc lều ở một trại hè với các kích thước trên hình ABC là tam giác vuông cân. Tính thể tích lều.

Câu 621 : Hình vẽ là chiếc lều ở một trại hè với các kích thước trên hình ABC là tam giác vuông cân. Số vải bạt cần có để dựng lều đó là bao nhiêu?

Câu 622 : Xét các hình sau:

Câu 623 : Xét các hình sau:

Câu 624 : Xét các hình sau:

Câu 625 : Xét các hình sau:

Câu 626 : Thể tích hình chóp đều cho theo các kích thước ở hình là:

Câu 627 : Tính thể tích hình chóp tứ giác đều O.ABCD các kích thước cho trên hình

Câu 628 : Hình chóp tứ giác đều có độ dài cạnh bên là 5cm, chiều cao hình chóp là 4cm. Thể tích của hình chóp là:

Câu 629 : Tính diện tích toàn phần của các hình chóp đều sau đây: Hình chóp tứ giác đều OA = 8cm,BC = CD = 6cm

Câu 630 : Tính diện tích toàn phần của các hình chóp đều sau đây: Hình chóp tứ giác đếu cạnh đáy 6cm, chiều cao hình chóp 5cm.

Câu 631 : Tính diện tích toàn phần của các hình chóp đều sau đây: Hình chóp tứ giác đều cạnh đáỵ 20cm, chiều cao hình chóp 7cm

Câu 632 : Tính diện tích toàn phần của các hình chóp đều sau đây: Hình chóp tứ giác đều cạnh đáỵ 1m, chiều cao hình chóp 50cm

Câu 633 : Tính thể tích và diện tích toàn phần của hình chóp đều dưới đây theo kích thước cho trên hình

Câu 634 : Tính thể tích và diện tích toàn phần của hình chóp đều dưới đây theo kích thước cho trên hình

Câu 635 : Tính diện tích toàn phần của hình chóp cụt đều theo các kích thước cho trên hình

Câu 636 : Cho hình chóp cụt tứ giác đều $A B C D . A_{1} B_{1} C_{1} D_{1}$ có các cạnh đáy 5cm và 10cm, đường cao mặt bên bằng 5cm. Hãy tính: Diện tích xung quanh của hình chóp cụt.

Câu 637 : Cho hình chóp cụt tứ giác đều $A B C D . A_{1} B_{1} C_{1} D_{1}$ có các cạnh đáy 5cm và 10cm, đường cao mặt bên bằng 5cm. Hãy tính: Tính cạnh bên và đường cao hình chóp cụt.

Câu 638 : Xét hình lập phương. Hãy chỉ ra: Hai đường thằng cắt nhau

Câu 639 : Xét hình lập phương. Hãy chỉ ra: Hai đường thẳng song song

Câu 640 : Xét hình lập phương. Hãy chỉ ra: Hai đường thẳng cẳt nhau và không cùng nằm trong một mặt phẳng

Câu 641 : Xét hình lập phương. Hãy chỉ ra: Hai đường thẳng cẳt nhau và không cùng nằm trong một mặt phẳng

Câu 642 : Xét hình lập phương. Hãy chỉ ra: Hai đường thẳng cẳt nhau và không cùng nằm trong một mặt phẳng

Câu 643 : Xét hình lập phương. Hãy chỉ ra: Hai đường thẳng cẳt nhau và không cùng nằm trong một mặt phẳng

Câu 644 : Trên hình vẽ, l, V, h là ba kích thước của hình hộp chữ nhật. Hãy điền số thích hợp vào ô trống ở bảng sau:

Câu 645 : Bồn đựng nước có dạng hình lăng trụ đứng các kích thước cho trên hình. Tính diện tích bề mặt của bồn (không tính nắp).

Câu 646 : Bồn đựng nước có dạng hình lăng trụ đứng các kích thước cho trên hình. Tính thể tích của bồn.

Câu 647 : Bồn đựng nước có dạng hình lăng trụ đứng các kích thước cho trên hìnBh. Khi bồn đầy ắp nước thì nó chứa được bao nhiêu ?

Câu 648 : Bồn đựng nước có dạng hình lăng trụ đứng các kích thước cho trên hình. Lượng sơn cần thiết để sơn cả mặt trong và mặt ngoài của bồn là bao nhiêu (một lít sơn phủ được 16 mét vông).

Câu 649 : Bồn đựng nước có dạng hình lăng trụ đứng các kích thước cho trên hình. Một vòi bơm với công suất 125 lít/phút để bơm một lượng nước vào bồn lên độ ccao cách đáy bồn là 1,05m thì phải mất bao lâu?

Câu 650 : Tính diện tích toàn phần của lăng trụ đứng theo các kích thước cho ở hình.

Câu 651 : Thùng của một xe tải có dạng hình lăng trụ đứng các kích thước cho ở trên hình. Tính thể tích của thùng chứa

Câu 652 : Thùng của một xe tải có dạng hình lăng trụ đứng các kích thước cho ở trên hình. Nếu 1( $m^{2}$ ) khối cát nặng 1,6 tấn và xe chở đến 34 trọng tải của nó thì sức nặng của cát lúc đó là bao nhiêu?

Câu 653 : Thùng của một xe tải có dạng hình lăng trụ đứng các kích thước cho ở trên hình. Khi cát được san phẳng chở đầy thì phần diện tích của nó bể trong thùng là bao nhiêu?

Câu 654 : Độ dài đường chéo AC1 của một hình lập phương là $\sqrt{12}$ . Độ dài mỗi cạnh là bao nhiêu?

Câu 655 : Độ dài đường chéo AC1 của một hình lập phương là $\sqrt{12}$ . Tính diện tích toàn phần và thể tích của hình lập phương.

Câu 656 : Hãy quan sát ba hình dưới đây,trong đó các hình vuông đơn vị được xếp theo dạng hình chữ U.Số hình lập phương đã xếp tăng lên theo quy luật 5 hình -> 28 hình ->81 hình.Nếu theo quy luật này thì có bao nhiêu hình lập phương đơn vị ở hình thứ 10?

Câu 657 : Hãy tìm diện tích mặt ngoài theo các kích thước cho ở hình.Biết rằng hình gồm một hình chóp đều và một hình hộp chữ nhật hình.

Câu 658 : Hãy tìm diện tích mặt ngoài theo các kích thước cho ở hình.Biết rằng hình gồm hai hình chóp đều

Câu 659 : Số hình lập phương đơn vị có ở hình bên là bao nhiêu?

Câu 660 : Cho biết hộp có dạng hình hộp chữ nhật ,độ dài đường chéo là 50.Hãy tìm các cạnh thước của hình hộp như vậy Hướng dẫn: Đây là bài toán mở hãy chọn hai trong ba kích thước của hình hộp có thể chấp nhận được từ đó tính kích thước còn lại

Câu 661 : Một hình lăng trụ đứng có đáy là tam giác vuông, chiều cao 7cm, độ dài hai cạnh góc vuông đáy là 3cm và 3cm. Hãy tính: Diện tích một mặt đáy

Câu 662 : Một hình lăng trụ đứng có đáy là tam giác vuông, chiều cao 7cm, độ dài hai cạnh góc vuông đáy là 3cm và 3cm. Hãy tính: Diện tích mặt xung quanh.

Câu 663 : Một hình lăng trụ đứng có đáy là tam giác vuông, chiều cao 7cm, độ dài hai cạnh góc vuông đáy là 3cm và 3cm. Hãy tính: Diện tích toàn phần.

Câu 664 : Một hình lăng trụ đứng có đáy là tam giác vuông, chiều cao 7cm, độ dài hai cạnh góc vuông đáy là 3cm và 3cm. Hãy tính: Thể tích lăng trụ.

Câu 665 : Tìm diện tích toàn phần và thể tích của hình lăng trụ đứng có kích thước như hình vẽ.

Câu 666 : Một hình chóp tứ giác đều S.ABCD có đọ dài cạnh đáy là 10cm,chiều có hình chóp là 12 cm.Tính : Diện tích toàn phần của hình chóp

Câu 667 : Một hình chóp tứ giác đều S.ABCD có đọ dài cạnh đáy là 10cm,chiều có hình chóp là 12 cm.Tính : Thể tích của hình chóp

Câu 668 : Người ta vẽ phần trên của một cái bàn học có dạng một lăng trụ đứng như hình vẽ các kích thước của nó là: AB= 108cm,BC =24cm; BF = 90 cm, FH =54 cm, LG=18 cm, LC = 78cm.Các cạnh AB,DC,EF,HG và KL đều vuông góc với mặt phẳng (ADKHE) và LG song song với BF.Hãy tính: Diện tích hình chữ nhật CDKL

Câu 669 : Người ta vẽ phần trên của một cái bàn học có dạng một lăng trụ đứng như hình vẽ các kích thước của nó là: AB= 108cm,BC =24cm; BF = 90 cm, FH =54 cm, LG=18 cm, LC = 78cm.Các cạnh AB,DC,EF,HG và KL đều vuông góc với mặt phẳng (ADKHE) và LG song song với BF.Hãy tính: Diện tích hình thang BCLGF

Câu 670 : Người ta vẽ phần trên của một cái bàn học có dạng một lăng trụ đứng như hình vẽ các kích thước của nó là: AB= 108cm,BC =24cm; BF = 90 cm, FH =54 cm, LG=18 cm, LC = 78cm.Các cạnh AB,DC,EF,HG và KL đều vuông góc với mặt phẳng (ADKHE) và LG song song với BF.Hãy tính: Thể tích hình lăng trụ đứng ADKHE.BCLGF

Câu 671 : Thể tích của hình chóp đều là 126 $c m^{3}$ ,chiều cao hình chóp là 6cm.Như vậy trong các số dưới đây ,số nào là diện tích đáy của nó?

Câu 672 : Cho hình chóp cụt đều ABCD.A'B'C'D' có cạnh đáy là a và 2a chiều cao của mặt bên là a. Tính diện tích xung quanh hình chóp cụt

Câu 673 : Cho hình chóp cụt đều ABCD.A'B'C'D' có cạnh đáy là a và 2a chiều cao của mặt bên là a. Tính đọ dài cạnh bên và chiều cao hình chóp cụt

Câu 674 : Cần phải đo đường chéo của một viên gạch có dạng hình hộp chữ nhật mà chỉ được phép sử dụng thước có chia vạch thì phải làm như thế nào?

Câu 675 : Tính thể tích của 1 trụ bê tông cho theo các kích thước ở hình, SJ = 9, OI = IJ. Phần trên là một hình hộp chữ nhật, phần dưới là một hình chóp cụt đều.

Câu 676 : Quan sát hình lăng trụ đứng tam giác ở hình bs.15 rồi điền số thích hợp vào các ô trống trong bảng sau:

Câu 677 : Một con kiến đang ở vị trí M là trung điểm cạnh A'D' của một chiếc hộp hình lập phương ABCD.A'B'C'D' (h. bs.16). Con kiến muốn bò qua sáu mặt của chiếc hộp rồi quay trở về M. Tìm đường đi ngắn nhất của con kiến.

Câu 678 : Thể tích của một hình chóp tam giác đều thay đổi thế nào nếu ta tăng. Gấp đôi chiều cao của hình chóp

Câu 679 : Thể tích của một hình chóp tam giác đều thay đổi thế nào nếu ta tăng. Gấp đôi cạnh đáy của hình chóp

Câu 680 : Thể tích của một hình chóp tam giác đều thay đổi thế nào nếu ta tăng. Gấp đôi cả chiều cao và cạnh đáy của hình chóp.

Câu 681 : Quan sát hình chóp tứ giác đều ở hình bs.17 rồi điền số thích hợp vào các ô trống trong bảng sau:

Câu 682 : Cho hình chóp cụt đều có đáy là hình vuông, các cạnh đáy là a và b. Biết diện tích xung quanh bằng tổng diện tích hai đáy, tính chiều cao của hình chóp cụt đều.

Câu 683 : Phân tích các đa thức sau thành nhân tử: $x^{2} + 2 x - 15 y^{2}$

Câu 684 : Phân tích các đa thức sau thành nhân tử: $x^{2}$ y + x $y^{2}$ + $x^{2}$ z + x $z^{2}$ + $y^{2}$ z + y $z^{2}$ + 3xyz.

Câu 685 : Cho biểu thức $P = {(x + 2)}^{2} - 2 (x + 2) (x - 8) + {(x - 8)}^{2}$ . Tính nhanh giá trị của biểu thức P tại x = -53/4.

Câu 686 : Chứng minh rằng với mọi số nguyên tố n ta có:

Câu 687 : Làm phép chia: (2 – 4x + 3 $x^{4}$ + 7 $x^{2}$ - 5 $x^{3}$ ) : (1 + $x^{2}$ – x).

Câu 688 : Chứng minh rằng thương tìm được trong phép chia ở câu a) luôn luôn dương với mọi giá trị x.

Câu 689 : Cho phân thức $P = \frac{x^{2} + y^{2}}{2 x + 3 y + 4}$ Với giá trị nào của x và y thì P = 0?

Câu 690 : Cho biểu thức $M = (\frac{x + 2}{3 x} + \frac{2}{x + 1} - 3) : \frac{2 - 4 x}{x + 1} - \frac{3 x - x^{2} + 1}{3 x}$

Câu 691 : Cho biểu thức $M = (\frac{x + 2}{3 x} + \frac{2}{x + 1} - 3) : \frac{2 - 4 x}{x + 1} - \frac{3 x - x^{2} + 1}{3 x}$

Câu 692 : Cho phương trình: 5(m + 3x)(x + 1) – 4(1 + 2x) = 80

Câu 693 : Trong hai nghiệm của phương trình

Câu 694 : Giải phương trình: $\frac{6}{x - 1} - \frac{4}{x - 3} + \frac{8}{(x - 1) (x - 3)} = 0$

Câu 695 : Giải bài toán bằng cách lập phương trình:

Câu 696 : Nghiệm của bất phương trình -4x + 12 < 0 là:

Câu 697 : Tìm các giá trị nguyên của x nghiệm đúng cả hai bất phương trình sau:

Câu 698 : Cho hình bình hành ABCD. O là giao điểm của hai đường chéo. Trên các cạnh AB, BC, CD, DA ta lần lượt lấy các điểm E, F, G, H sao cho AE = CG, BF = DH. Xác định tâm đối xứng của hình bình hành ABCD.

Câu 699 : Cho hình bình hành ABCD. O là giao điểm của hai đường chéo. Trên các cạnh AB, BC, CD, DA ta lần lượt lấy các điểm E, F, G, H sao cho AE = CG, BF = DH. Chứng minh EFGH là hình bình hành, tìm tâm đối xứng của nó.

Câu 700 : Cho hình bình hành ABCD. O là giao điểm của hai đường chéo. Trên các cạnh AB, BC, CD, DA ta lần lượt lấy các điểm E, F, G, H sao cho AE = CG, BF = DH. O còn là tâm đối xứng của những hình bình hành nào?

Câu 701 : Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q theo thứ tự là trung điểm của AB, AC, CD, BD. Chứng minh rằng MNPQ là hình bình hành.

Câu 702 : Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q theo thứ tự là trung điểm của AB, AC, CD, BD. Nếu ABCD là hình thang cân thì tứ giác MNPQ là hình gì? Vì sao?

Câu 703 : Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q theo thứ tự là trung điểm của AB, AC, CD, BD. Hình thang ABCD có thêm điều kiện gì thì MNPQ là hình vuông?

Câu 704 : Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B (A nằm giữa O và B), trên tia Oy lấy hai điểm C và D (C nằm giữa O và D). Gọi M, N, P, Q theo thứ tự là trung điểm của AC, BC, BD, và AD.

Câu 705 : Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B (A nằm giữa O và B), trên tia Oy lấy hai điểm C và D (C nằm giữa O và D). Gọi M, N, P, Q theo thứ tự là trung điểm của AC, BC, BD, và AD.

Câu 706 : Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B (A nằm giữa O và B), trên tia Oy lấy hai điểm C và D (C nằm giữa O và D). Gọi M, N, P, Q theo thứ tự là trung điểm của AC, BC, BD, và AD.

Câu 707 : Cho tam giác nhọn ABC (AC > AB), đường cao AH. Gọi D, E, F theo thứ tự là trung điểm của AB, AC, BC. Xác định dạng của tứ giác DECH, BDEF và DEFH.

Câu 708 : Cho tam giác nhọn ABC (AC > AB), đường cao AH. Gọi D, E, F theo thứ tự là trung điểm của AB, AC, BC. Biết AH = 8cm, HB = 4cm, HC = 6cm, tính diện tích các tứ giác DECH, BDEF và DEFH.

Câu 709 : Cho tam giác nhọn ABC (AC > AB), đường cao AH. Gọi D, E, F theo thứ tự là trung điểm của AB, AC, BC. Tính độ dài HE.

Câu 710 : Tứ giác ABCD có AB = 3cm, BC = 10cm, CD = 12cm, AD = 5cm, đường chéo BD = 6cm. Chứng minh rằng ABCD là hình thang.

Câu 711 : Cho tam giác ABC và các đường cao BD, CE. Tính số đo góc AED biết $∠$ (ACB) = $48^{0}$

Câu 712 : Một tam giác có độ dài ba cạnh là 6cm, 8cm và 13cm. Một tam giác khác đồng dạng với tam giác đã cho co độ dài ba cạnh là 12cm, 9cm và x (cm). Độ dài x là:

Câu 713 : Tam giác ABC vuông ở C có AC = 6cm, AB = 9cm, CD là đường cao (D ∈ AB). Độ dài BD bằng:

Câu 714 : Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = 4cm, AC = 5cm và A’C = 13cm. Tính thể tích và diện tích xung quanh của hình hộp chữ nhật đó.

Câu 715 : Hình chóp tứ giác đều S.ABCD có chiều cao 15cm và thể tích là 1280 $c m^{3}$ . Độ dài cạnh đáy của nó là:

Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).

Lớp 8

Toán học

Toán học - Lớp 8

Tiểu học Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Hóa học Tài liệu Đề thi & kiểm tra Câu hỏi hoctapsgk.com Nghe truyện audio Đọc truyện chữ Công thức nấu ăn

Giải Sách Bài Tập Toán 8 Tập 2 !!

Câu 1 : Trong các số -2; -1,5; -1; 0,5; 2/3 ;2 ;3 số nào là nghiệm của mỗi phương trình sau: y2-3=2y

Câu 2 : Trong các số -2; -1,5; -1; 0,5; 2/3 ;2 ;3 số nào là nghiệm của mỗi phương trình sau: t + 3 = 4 - t

Câu 3 : Trong các số -2; -1,5; -1; 0,5; 2/3 ;2 ;3 số nào là nghiệm của mỗi phương trình sau: 3x-42+1=0

Câu 4 : Hãy thử lại và cho biết các khẳng định sau có đúng không: x3 + 3x = 2x2 – 3x + 1 ⇔ x=-1

Câu 5 : Hãy thử lại và cho biết các khẳng định sau có đúng không: z – 2z2+1= 2z + 5 ⇔ z = 3

Câu 6 : Cho ba biểu thức 5x – 3; x2-3x+12 và (x + 1)(x – 3)

Câu 7 : Cho ba biểu thức 5x – 3; x2-3x+12 và (x + 1)(x – 3)

Câu 9 : Thử lại rằng phương trình 2mx - 5 = - x + 6m - 2 luôn luôn nhận x = 3 là nghiệm, dù m lấy bât cứ giá trị nào.

Câu 10 : Cho hai phương trình x2-5x+6=0 (1) và x + (x - 2)(2x + 1) = 2 (2)

Câu 11 : Cho hai phương trình x2-5x+6=0 (1) và x + (x - 2)(2x + 1) = 2 (2)

Câu 12 : F

Câu 13 : Tại sao có thể kết luận tập nghiệm của phương trình x+1=2-x là ∅?

Câu 14 : Chứng minh rằng phương trình x + |x| = 0 nghiệm đúng với mọi x ≤ 0

Câu 15 : Cho phương trình m2+5m+4x2=m+4, trong đó m là một số. Chứng minh rằng: Khi m = - 4, phương trình nghiệm đúng với mọi giá trị của ẩn

Câu 16 : Cho phương trình m2+5m+4x2=m+4, trong đó m là một số. Chứng minh rằng: Khi m = - l, phương trình nghiệm vô nghiệm.

Câu 17 : Cho phương trình m2+5m+4x2=m+4, trong đó m là một số. Chứng minh rằng: Khi m = - 2 hoặc m = -3, phương trình vô nghiệm.

Câu 18 : Cho phương trình m2+5m+4x2=m+4, trong đó m là một số. Chứng minh rằng: Khi m = 0 phương trình nhận x = l và x = - l là nghiệm.

Câu 19 : Bằng quy tắc chuyển vế, giải các phương trình sau: x – 2,25 = 0,75

Câu 20 : Bằng quy tắc chuyển vế, giải các phương trình sau: 19,3 = 12 – x

Câu 21 : Bằng quy tắc chuyển vế, giải các phương trình sau: 4,2 = x + 2,1

Câu 22 : Bằng quy tắc chuyển vế, giải các phương trình sau: 3,7 – x = 4

Câu 23 : Bằng quy tắc nhân, tìm giá trị gần đúng nghiệm của các phương trình sau (làm tròn đến chữ số thập phân thứ ba). 2x = 13

Câu 24 : Bằng quy tắc nhân, tìm giá trị gần đúng nghiệm của các phương trình sau (làm tròn đến chữ số thập phân thứ ba). x2 = 43

Câu 25 : Bằng quy tắc nhân, tìm giá trị gần đúng nghiệm của các phương trình sau (làm tròn đến chữ số thập phân thứ ba). –5x = 1 + 5

Câu 26 : Tìm giá trị của m sao cho phương trình sau đây nhận x = -2 là nghiệm: 2x + m = x – 1

Câu 27 : Tìm giá trị của k, biết rắng một trong hai phương trình sau đây nhận x = 5 là nghiệm, phương trình còn lại nhận x = -1 là nghiệm: 2x = 10 và 3 – kx = 2

Câu 28 : Giải các phương trình sau: 7x + 21 = 0

Câu 29 : Giải các phương trình sau: 5x – 2 = 0

Câu 30 : Giải các phương trình sau: 12 – 6x = 0

Câu 31 : Giải các phương trình sau: -2x + 14 = 0

Câu 32 : Giải các phương trình sau: 0,25x + 1,5 = 0

Câu 33 : Giải các phương trình sau: 6,36 – 5,3x = 0

Câu 34 : Giải các phương trình sau: 4/3 x - 5/6 = 1/2

Câu 35 : Giải các phương trình sau: -5/9 x + 1 = 2/3 x – 10

Câu 36 : Giải các phương trình sau: 3x + 1 = 7x – 11

Câu 37 : Giải các phương trình sau: 5 – 3x = 6x + 7

Câu 38 : Giải các phương trình sau: 11 – 2x = x – 1

Câu 39 : Giải các phương trình sau: 15 – 8x = 9 – 5x

Câu 40 : Chứng tỏ rằng các phương trình sau đây vô nghiệm: 2(x + 1) = 3 + 2x

Câu 41 : Chứng tỏ rằng các phương trình sau đây vô nghiệm: 2(1 – 1,5x) + 3x = 0

Câu 42 : Chứng tỏ rằng các phương trình sau đây vô nghiệm: |x| = -1

Câu 43 : Cho phương trình m-4x+2=m. Giải phương trình trong mỗi trường hợp sau: m = 2

Câu 44 : Cho phương trình m-4x+2=m. Giải phương trình trong mỗi trường hợp sau: m = -2

Câu 45 : Cho phương trình m-4x+2=m. Giải phương trình trong mỗi trường hợp sau: m = -2,2

Câu 46 : Giải các phương trình sau: 1,2 – (x – 0,8) = -2(0,9 + x)

Câu 47 : Giải các phương trình sau: 2,3x – 2(0,7 + 2x) = 3,6 – 1,7x

Câu 48 : Giải các phương trình sau: 3(2,2 – 0,3x) = 2,6 + (0,1x – 4)

Câu 49 : Giải các phương trình sau: 3,6 – 0,5(2x + 1) = x – 0,25(2 – 4x)

Câu 50 : Giải các phương trình sau x-35=6-1-2x3

Câu 51 : Giải các phương trình sau: 3x-26-5=3-2x+74

Câu 52 : Giải các phương trình sau: 2x+35=5-135+x

Câu 53 : Giải các phương trình sau: 7x8-5x-9=20x+1,56

Câu 54 : Tìm điều kiện của x để giá trị mỗi phân thức sau xác định: A=3x+22x-1-32x+1

Câu 55 : Tìm điều kiện của x để giá trị mỗi phân thức sau xác định: B=0,5x+3-21,2x+0,7-40,6x+0,9)

Câu 56 : Giải các phương trình sau: 5x-1+26-7x-14=22x+17-5

Câu 57 : Giải các phương trình sau: 3x-34+4x-10,510=3x+15+6

Câu 58 : Giải các phương trình sau: 23x+1+14-5=23x-15-3x+210

Câu 59 : Giải các phương trình sau: x+13+32x+14=2x+3x+16+7+12x12

Câu 60 : Tìm giá trị của k sao cho: Phương trình (2x + 1)(9x + 2k) – 5(x + 2) = 40 có nghiệm x = 2.

Câu 61 : Tìm giá trị của k sao cho: Phương trình 2(2x + 1) + 18 = 3(x + 2)(2x + k) có nghiệm x = 1.

Câu 62 : Tìm các giá trị của x sao cho hai biểu thức A và B cho sau đây có giá trị bằng nhau: A = (x – 3)(x + 4) – 2(3x – 2); B = x-42

Câu 63 : Tìm các giá trị của x sao cho hai biểu thức A và B cho sau đây có giá trị bằng nhau: A = (x + 2)(x – 2) + 3x2; B = 2x+12 + 2x

Câu 64 : Tìm các giá trị của x sao cho hai biểu thức A và B cho sau đây có giá trị bằng nhau: A = (x – 1)(x2 + x + 1) – 2x; B = x(x – 1)(x + 1)

Câu 65 : Tìm các giá trị của x sao cho hai biểu thức A và B cho sau đây có giá trị bằng nhau: A = x+13 – x-23; B = (3x – 1)(3x + 1)

Câu 66 : Giải các phương trình sau: 2x3+2x-16=4-x3

Câu 67 : Giải các phương trình sau: x-12+x-14=1-2x-12

Câu 68 : Giải các phương trình sau: 2-x2001-1=1-x2002-x2003

Câu 69 : Cho hai phương trình:

Câu 70 : Cho hai phương trình:

Câu 71 : Cho hai phương trình:

Câu 72 : Bằng cách đặt ẩn phụ theo hướng dẫn, giải các phương trình sau: 616x+37-8=316x+37+7

Câu 73 : Bằng cách đặt ẩn phụ theo hướng dẫn, giải các phương trình sau: 2+2x2-1=2x2-2

Câu 74 : Bằng cách đặt ẩn phụ theo hướng dẫn, giải các phương trình sau:0,052x-22009+2x2010+2x+22011=3,3-x-12009+x2010+x+12011

Câu 75 : Giải các phương trình sau: (4x – 10)(24 + 5x) = 0

Câu 76 : Giải các phương trình sau: (3,5 – 7x)(0,1x + 2,3) = 0

Câu 77 : Giải các phương trình sau: 3x-22x+37-4x-35=0

Câu 78 : Giải các phương trình sau: 3,3-11x7x+25+21-3x3=0

Câu 79 : Dùng máy tính bỏ túi để tính giá trị gần đúng các nghiệm của mỗi phương trình sau, làm tròn đến chữ số thập phân thứ ba. (3 - x5 )(2x2 + 1) = 0

Câu 80 : Dùng máy tính bỏ túi để tính giá trị gần đúng các nghiệm của mỗi phương trình sau, làm tròn đến chữ số thập phân thứ ba. (2x - 7 )(x10 + 3) = 0

Câu 1 : Trong các số -2; -1,5; -1; 0,5; 2/3 ;2 ;3 số nào là nghiệm của mỗi phương trình sau: $y^{2} - 3 = 2 y$

Câu 3 : Trong các số -2; -1,5; -1; 0,5; 2/3 ;2 ;3 số nào là nghiệm của mỗi phương trình sau: $\frac{3 x - 4}{2} + 1 = 0$

Câu 4 : Hãy thử lại và cho biết các khẳng định sau có đúng không: $x^{3} + 3 x = 2 x^{2} - 3 x + 1 \Leftrightarrow x = - 1$

Câu 5 : Hãy thử lại và cho biết các khẳng định sau có đúng không: $(z - 2) (z^{2} + 1) = 2 z + 5 \Leftrightarrow z = 3$

Câu 6 : Cho ba biểu thức 5x – 3; $x^{2} - 3 x + 12$ và (x + 1)(x – 3)

Câu 7 : Cho ba biểu thức 5x – 3; $x^{2} - 3 x + 12$ và (x + 1)(x – 3)

Câu 10 : Cho hai phương trình $x^{2} - 5 x + 6 = 0$ (1) và x + (x - 2)(2x + 1) = 2 (2)

Câu 11 : Cho hai phương trình $x^{2} - 5 x + 6 = 0$ (1) và x + (x - 2)(2x + 1) = 2 (2)

Câu 13 : Tại sao có thể kết luận tập nghiệm của phương trình $\sqrt{x} + 1 = 2 \sqrt{- x}$ là ∅?

Câu 15 : Cho phương trình $(m^{2} + 5 m + 4) x^{2} = m + 4$ , trong đó m là một số. Chứng minh rằng: Khi m = - 4, phương trình nghiệm đúng với mọi giá trị của ẩn

Câu 16 : Cho phương trình $(m^{2} + 5 m + 4) x^{2} = m + 4$ , trong đó m là một số. Chứng minh rằng: Khi m = - l, phương trình nghiệm vô nghiệm.

Câu 17 : Cho phương trình $(m^{2} + 5 m + 4) x^{2} = m + 4$ , trong đó m là một số. Chứng minh rằng: Khi m = - 2 hoặc m = -3, phương trình vô nghiệm.

Câu 18 : Cho phương trình $(m^{2} + 5 m + 4) x^{2} = m + 4$ , trong đó m là một số. Chứng minh rằng: Khi m = 0 phương trình nhận x = l và x = - l là nghiệm.

Câu 23 : Bằng quy tắc nhân, tìm giá trị gần đúng nghiệm của các phương trình sau (làm tròn đến chữ số thập phân thứ ba). 2x = $\sqrt{13}$

Câu 24 : Bằng quy tắc nhân, tìm giá trị gần đúng nghiệm của các phương trình sau (làm tròn đến chữ số thập phân thứ ba). x $\sqrt{2}$ = 4 $\sqrt{3}$

Câu 25 : Bằng quy tắc nhân, tìm giá trị gần đúng nghiệm của các phương trình sau (làm tròn đến chữ số thập phân thứ ba). –5x = 1 + $\sqrt{5}$

Câu 43 : Cho phương trình $(m^{} - 4) x + 2 = m$ . Giải phương trình trong mỗi trường hợp sau: m = 2

Câu 44 : Cho phương trình $(m^{} - 4) x + 2 = m$ . Giải phương trình trong mỗi trường hợp sau: m = -2

Câu 45 : Cho phương trình $(m^{} - 4) x + 2 = m$ . Giải phương trình trong mỗi trường hợp sau: m = -2,2

Câu 50 : Giải các phương trình sau $\frac{x - 3}{5} = 6 - \frac{1 - 2 x}{3}$

Câu 51 : Giải các phương trình sau: $\frac{3 x - 2}{6} - 5 = \frac{3 - 2 (x + 7)}{4}$

Câu 52 : Giải các phương trình sau: $2 (x + \frac{3}{5}) = 5 - (\frac{13}{5} + x)$

Câu 53 : Giải các phương trình sau: $\frac{7 x}{8} - 5 (x - 9) = \frac{20 x + 1, 5}{6}$

Câu 54 : Tìm điều kiện của x để giá trị mỗi phân thức sau xác định: $A = \frac{3 x + 2}{2 (x - 1) - 3 (2 x + 1)}$

Câu 55 : Tìm điều kiện của x để giá trị mỗi phân thức sau xác định: $B = \frac{(0, 5 (x + 3) - 2)}{(1, 2 (x + 0, 7)) - 4 (0, 6 x + 0, 9))}$

Câu 56 : Giải các phương trình sau: $\frac{5 (x - 1) + 2}{6} - \frac{7 x - 1}{4} = \frac{2 (2 x + 1)}{7} - 5$

Câu 57 : Giải các phương trình sau: $\frac{3 (x - 3)}{4} + \frac{4 x - 10, 5}{10} = \frac{3 (x + 1)}{5} + 6$

Câu 58 : Giải các phương trình sau: $\frac{2 (3 x + 1) + 1}{4} - 5 = \frac{2 (3 x - 1)}{5} - \frac{3 x + 2}{10}$

Câu 59 : Giải các phương trình sau: $\frac{x + 1}{3} + \frac{3 (2 x + 1)}{4} = \frac{2 x + 3 (x + 1)}{6} + \frac{7 + 12 x}{12}$

Câu 62 : Tìm các giá trị của x sao cho hai biểu thức A và B cho sau đây có giá trị bằng nhau: A = (x – 3)(x + 4) – 2(3x – 2); B = ${(x - 4)}^{2}$

Câu 63 : Tìm các giá trị của x sao cho hai biểu thức A và B cho sau đây có giá trị bằng nhau: A = (x + 2)(x – 2) + 3 $x^{2}$ ; B = ${(2 x + 1)}^{2}$ + 2x

Câu 64 : Tìm các giá trị của x sao cho hai biểu thức A và B cho sau đây có giá trị bằng nhau: A = (x – 1)( $x^{2}$ + x + 1) – 2x; B = x(x – 1)(x + 1)

Câu 65 : Tìm các giá trị của x sao cho hai biểu thức A và B cho sau đây có giá trị bằng nhau: A = ${(x + 1)}^{3}$ – ${(x - 2)}^{3}$ ; B = (3x – 1)(3x + 1)

Câu 66 : Giải các phương trình sau: $\frac{2 x}{3} + \frac{2 x - 1}{6} = 4 - \frac{x}{3}$

Câu 67 : Giải các phương trình sau: $\frac{x - 1}{2} + \frac{x - 1}{4} = 1 - \frac{2 (x - 1)}{2}$

Câu 68 : Giải các phương trình sau: $\frac{2 - x}{2001} - 1 = \frac{1 - x}{2002} - \frac{x}{2003}$

Câu 72 : Bằng cách đặt ẩn phụ theo hướng dẫn, giải các phương trình sau: $\frac{6 (16 x + 3)}{7} - 8 = \frac{3 (16 x + 3)}{7} + 7$

Câu 73 : Bằng cách đặt ẩn phụ theo hướng dẫn, giải các phương trình sau: $(\sqrt{2} + 2) (x \sqrt{2} - 1) = 2 x \sqrt{2} - \sqrt{2}$

Câu 74 : Bằng cách đặt ẩn phụ theo hướng dẫn, giải các phương trình sau: $0, 05 (\frac{2 x - 2}{2009} + \frac{2 x}{2010} + \frac{2 x + 2}{2011}) = 3, 3 - (\frac{x - 1}{2009} + \frac{x}{2010} + \frac{x + 1}{2011})$

Câu 77 : Giải các phương trình sau: $(3 x - 2) [\frac{2 (x + 3)}{7} - \frac{4 x - 3}{5}] = 0$

Câu 78 : Giải các phương trình sau: $(3, 3 - 11 x) [\frac{7 x + 2}{5} + \frac{2 (1 - 3 x)}{3}] = 0$

Câu 79 : Dùng máy tính bỏ túi để tính giá trị gần đúng các nghiệm của mỗi phương trình sau, làm tròn đến chữ số thập phân thứ ba. ( $\sqrt{3}$ - x $\sqrt{5}$ )(2x $\sqrt{2}$ + 1) = 0

Câu 80 : Dùng máy tính bỏ túi để tính giá trị gần đúng các nghiệm của mỗi phương trình sau, làm tròn đến chữ số thập phân thứ ba. (2x - $\sqrt{7}$ )(x $\sqrt{10}$ + 3) = 0

Câu 81 : Dùng máy tính bỏ túi để tính giá trị gần đúng các nghiệm của mỗi phương trình sau, làm tròn đến chữ số thập phân thứ ba. (2 – 3x $\sqrt{5}$ )(2,5x + $\sqrt{2}$ ) = 0

Câu 82 : Dùng máy tính bỏ túi để tính giá trị gần đúng các nghiệm của mỗi phương trình sau, làm tròn đến chữ số thập phân thứ ba. ( $\sqrt{13}$ + 5x)(3,4 – 4x $\sqrt{1, 7}$ ) =

Câu 86 : Giải các phương trình sau: ${(2 x - 1)}^{2}$ + (2 – x)(2x – 1) = 0

Câu 87 : Giải các phương trình sau: (x + 2)(3 – 4x) = $x^{2}$ + 4x + 4

Câu 88 : Giải các phương trình sau: $x^{2}$ + (x + 2)(11x - 7) = 4

Câu 89 : Giải các phương trình sau: (x – 1)( $x^{2}$ + 5x – 2) – ( $x^{3}$ – 1) = 0

Câu 90 : Giải các phương trình sau: $x^{3}$ + 1 = x(x + 1)

Câu 91 : Giải các phương trình bậc hai sau đây bằng cách đưa về dạng phương trình tích: $x^{2}$ – 3x + 2 = 0

Câu 92 : Giải các phương trình bậc hai sau đây bằng cách đưa về dạng phương trình tích: – $x^{2}$ + 5x – 6 = 0

Câu 93 : Giải các phương trình bậc hai sau đây bằng cách đưa về dạng phương trình tích: 2 $x^{2}$ + 5x + 3 = 0

Câu 94 : Giải các phương trình bậc hai sau đây bằng cách đưa về dạng phương trình tích: 4 $x^{2}$ – 12x + 5 = 0

Câu 95 : Giải các phương trình bằng cách đưa về dạng phương trình tích: (x - $\sqrt{2}$ ) + 3( $x^{2}$ – 2) = 0

Câu 96 : Giải các phương trình bằng cách đưa về dạng phương trình tích: $x^{2}$ – 5 = (2x - $\sqrt{5}$ )(x + $\sqrt{5}$ )

Câu 99 : Biết x = - 2 là một trong các nghiệm của phương trình: $x^{3} + a x^{2} - 4 x - 4 = 0$ . Xác định giá trị của a.

Câu 101 : Biết x = - 2 là một trong các nghiệm của phương trình: $x^{3} + a x^{2} - 4 x - 4 = 0$ . Với a tìm được ở câu a, tìm các nghiêm còn lại của phương trình bằng cách đưa phương trình đã cho về dạng phương trình tích.

Câu 104 : Khi giải phương trình $\frac{2 - 3 x}{- 2 x - 3} = \frac{3 x + 2}{2 x + 1}$ , bạn Hà làm như sau:

Câu 106 : Giải các phương trình sau: $\frac{1 - x}{x + 1} + 3 = \frac{2 x + 3}{x + 1}$

Câu 107 : Giải các phương trình sau: $\frac{{(x + 2)}^{2}}{2 x - 3} - 1 = \frac{x^{2} + 10}{2 x - 3}$

Câu 108 : Giải các phương trình sau: $\frac{5 x - 2}{2 - 2 x} + \frac{2 x - 1}{2} = 1 - \frac{x^{2} + x - 3}{1 - x}$

Câu 109 : Giải các phương trình sau: $\frac{5 - 2 x}{3} + \frac{(x + 1) (x - 1)}{3 x - 1} = \frac{(x + 2) (1 - 3 x)}{9 x - 3}$

Câu 110 : Tìm x sao cho biểu thức $\frac{2 x^{2} - 3 x - 2}{x^{2} - 4}$ bằng 2.

Câu 111 : Tìm x sao cho giá trị của hai biểu thức sau bằng nhau: $\frac{6 x - 1}{3 x + 2} v à \frac{2 x + 5}{x - 3}$

Câu 112 : Tìm y sao cho giá trị của hai biểu thức sau bằng nhau: $\frac{y + 5}{y - 1} - \frac{y + 1}{y - 3} v à \frac{- 8}{(y - 1) (y - 3)}$

Câu 113 : Giải các phương trình sau: $\frac{1 - 6 x}{x - 2} + \frac{9 x + 4}{x + 2} = \frac{x (3 x - 2) + 1}{x^{2} - 4}$

Câu 114 : Giải các phương trình sau: $\frac{2}{x - 1} + \frac{2 x + 3}{x^{2} + x + 1} = \frac{(2 x - 1) (2 x + 1)}{x^{3} - 1}$

Câu 115 : Giải các phương trình sau: $1 + \frac{x}{3 - x} = \frac{5 x}{(x + 2) (3 - x)} + \frac{2}{x + 2}$

Câu 116 : Giải các phương trình sau: $\frac{x^{3} - {(x - 1)}^{3}}{(4 x + 3) (x - 5)} = \frac{7 x - 1}{4 x + 3} - \frac{x}{x - 5}$

Câu 117 : Giải các phương trình sau: $\frac{2 x + 1}{x - 1} = \frac{5 (x - 1)}{x + 1}$

Câu 118 : Giải các phương trình sau: $\frac{x - 3}{x - 2} + \frac{x - 2}{x - 4} = - 1$

Câu 119 : Giải các phương trình sau: $\frac{1}{x - 1} + \frac{2 x^{2} - 5}{x^{3} - 1} = \frac{4}{x^{2} + x + 1}$

Câu 120 : Giải các phương trình sau: $\frac{13}{(x - 3) (2 x + 7)} + \frac{1}{2 x + 7} = \frac{6}{x^{2} - 9}$

Câu 121 : Cho phương trình ẩn x: $\frac{x + a}{a - x} + \frac{x - a}{a + x} = \frac{a (3 a + 1)}{a^{2} - x^{2}}$

Câu 122 : Cho phương trình ẩn x: $\frac{x + a}{a - x} + \frac{x - a}{a + x} = \frac{a (3 a + 1)}{a^{2} - x^{2}}$

Câu 123 : Cho phương trình ẩn x: $\frac{x + a}{a - x} + \frac{x - a}{a + x} = \frac{a (3 a + 1)}{a^{2} - x^{2}}$