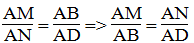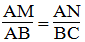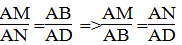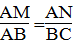Cho hình bình hành ABCD .Từ A kẻ AM vuông góc với BC,AN vuông
Câu hỏi :
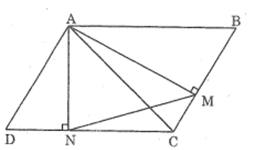
Cho hình bình hành ABCD .Từ A kẻ AM vuông góc với BC,AN vuông góc CD (M thuộc BC và N thuộc CD). Chứng mình rằng tam giác MAN đồng dạng với tam giác ABC.
* Đáp án
* Hướng dẫn giải
* Trường hợp góc B nhọn:
Xét AMB và AND, ta có:
(AMB) = (AND) =
B = D (t/chất hình bình hành) ⇒ AMB đồng dạng AND (g.g)
Suy ra:
Mà AD = BC (t/chất hình hình hành)
Suy ra:
Lại có: AB // CD (gt)
AN ⊥ CD (gt)
Suy ra: AN ⊥ AB hay (NAB) =
suy ra: NAM + MAB = (1)
Trong tam giác vuông AMB ta có ABM =
Suy ra: (MAB) + B = (2)
Từ (1) và (2) suy ra: NAM = B
Xét ABC và MAN ta có:
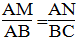
(NAM) = B (chứng minh trên)
Vậy ABC đồng dạng MAN (c.g.c)
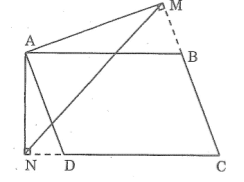
* Trường hợp góc B tù:
Xét MAN và AND, ta có:
(AMB) = (AND) =
(ABM) = (ADN) (vì cùng bằng C)
⇒AMB đông dạng AND (g.g)
Suy ra:
Mà AD = BC (t/chẩt hình bình hành)
Suy ra:
Vì AB //CD nên (ABC) + C = (3)
Tứ giác AMCN có (AMC) = (AND) =
Suy ra: (MAN) + C = (4)
Từ (3) và (4) suy ra: (MAN) = (ABC)
Xét AMN và ABC, ta có:
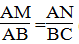
(MAN) = (ABC) (chứng minh trên)
Vậy MAN đồng dạng ABC (c.g.c)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 2 !!
Copyright © 2021 HOCTAP247