Giả sử AC là đường chéo lớn của hình bình hành ABCD. Từ C, vẽ

* Hướng dẫn giải

Dựng BG ⊥ AC.

Xét ΔBGA và ΔCEA, ta có:

$\angle$(BGA) = $\angle$(CEA) = ${90}^0$

$\angle$A chung

⇒$△$BGA đồng dạng $△$CEA(g.g)

Suy ra: 

AB.AE = AC.AG (1)

Xét $△$BGC và $△$CFA, ta có:

$\angle$(BGC) = $\angle$(CFA) = ${90}^0$

$\angle$(BCG) = $\angle$(CAF) (so le trong vì AD //BC)

$△$BGC đồng dạng $△$CFA (g.g)

Suy ra: 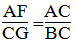 ⇒ BC.AF = AC.CG

Mà BC = AD (tính chất hình bình hành)

Suy ra: AD.AF = AC.CG (2)

Cộng từng vế đẳng thức (1) và (2) ta có:

AB.AE + AD.AF = AC.AG + AC.CG

AB.AE + AD.AF= AC(AG + CG)

Mà AG + CG = AC nên AB.AE + AD.AF = $A{C}^2$