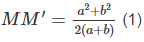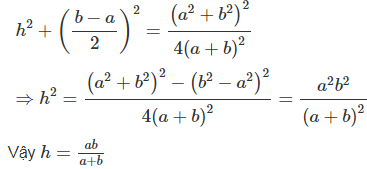Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải Sách Bài Tập Toán 8 Tập 2 !!
Cho hình chóp cụt đều có đáy là hình vuông,...
Cho hình chóp cụt đều có đáy là hình vuông, các cạnh đáy là a và b
Câu hỏi :
Cho hình chóp cụt đều có đáy là hình vuông, các cạnh đáy là a và b. Biết diện tích xung quanh bằng tổng diện tích hai đáy, tính chiều cao của hình chóp cụt đều.
* Đáp án
* Hướng dẫn giải
Xét hình chóp cụt đều ABCD.A'B'C'D' như hình bs.19.
Gọi M, M' thứ tự là trung điểm của BC, B'C'. Khi đó MM' là đường cao của hình thang cân BCC'B'.
Do đó diện tích xung quanh của hình chóp cụt đều là:
= 4.(a+b)/2.MM′=(2a+2b).MM′
Từ giả thiết ta có:
(2a+2b).MM′=
Dễ thấy OM // O'M' nên OM và O'M' xác định mặt phẳng (OMM'O'). Trong mặt phẳng (OMM'O'), kẻ MH ⊥ O'M'. Khi đó: HM' = O'M' – O'H = (b−a)/2
Trong tam giác vuông MHM' ta có: (2)
Từ (1) và (2) suy ra :
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 2 !!
Số câu hỏi: 715
Copyright © 2021 HOCTAP247