Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải Sách Bài Tập Toán 8 Tập 1 !!
Cho hình vuông ABCD. Gọi M, N, P, Q tương...
Cho hình vuông ABCD. Gọi M, N, P, Q tương ứng là trung điểm của
Câu hỏi :
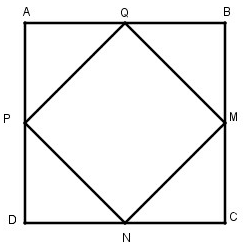
Cho hình vuông ABCD. Gọi M, N, P, Q tương ứng là trung điểm của các cạnh BC, CD, DA, AB. Chứng minh MNPQ là hình vuông (tứ giác đều)
* Đáp án
* Hướng dẫn giải
Do ABCD là hình vuông có M, N, P, Q lần lượt là trung điểm của BC, CD, DA, AB nên: AQ = QB = BM = MC= CN = ND = DP = PA
Xét Δ APQ và Δ BQM:
AQ = BM (gt)
A = B =
AP = BQ (gt)
Do đó: APQ = BQM (c.g.c) ⇒ PQ = QM (1)
Xét BQM và CMN:
BM = CN (gt)
B = C =
BQ = CM (gt)
Do đó: BQM = CMN (c.g.c) ⇒ QM = MN (2)
Xét CMN và DNP:
CN = DP (gt)
C = D =
CM = DN (gt)
Do đó: CMN = DNP (c.g.c) ⇒ MN = NP (3)
Từ (1), (2) và (3) suy ra: MN = NP = PQ = QM
nên tứ giác MNPQ là hình thoi
Vì AP = AQ nên APQ vuông cân tại A
BQ = BM nên BMQ vuông cân tại B
⇒ (AQP) = (BQM) =
(AQP) + (PQM) + (BQM) = (kề bù)
⇒ (PQM) = - ( (AQP) + (BQM) )
= - ( +) =
Vậy tứ giác MNPQ là hình vuông.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Số câu hỏi: 794
Copyright © 2021 HOCTAP247