Dùng diện tích để chứng tỏ : (a + b)^2 = a^2 + 2ab + b^2

* Hướng dẫn giải

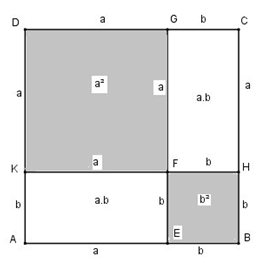
Dựng hình vuông ABCD có cạnh bằng (a + b )

Trên cạnh AB dựng điểm E sao cho AE = a, EB = b, trên cạnh BC dựng điểm H sao cho BH = b, HC = a, trên cạnh CD dựng điểm G sao cho CG = b, GD = a, trên cạnh DA dựng điểm K sao cho DK = a, KA = b, GE cắt KH tại F.

Ta có : diện tích hình vuông ABCD bằng ${\left(a+b\right)}^2$

Diện tích hình vuông DKFG bằng $a^2$

Diện tích hình chữ nhật AKFE bằng a.b

Diện tích hình vuông EBHF bằng $b^2$

Diện tích hình chữ nhật HCGF bằng a.b

$S_{ABCD}=S_{DKFG}+S_{AKEF}+S_{EBHF}+S_{HCGF}$

Vậy ta có : ${\left(a+b\right)}^2=a^2+2ab+b^2$