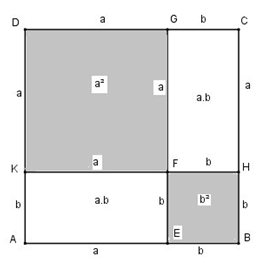
Dùng diện tích để chứng tỏ : (a- b)^2 = a^2 - 2ab + b^2 với điều kiện b < a

* Hướng dẫn giải

Dựng hình vuông ABCD có cạnh bằng a

Trên cạnh AB lấy điểm E sao cho BE = b

Từ E dựng đường thẳng song song BC cắt CD tại G

Ta có: CG = b, CE = ( a – b ), GD = ( a – b )

Trên cạnh AD lấy điểm K sao cho AK = b

Từ K kẻ đường thẳng song song với AB cắt BC tại H và cắt EG tại F

Ta có: KD = ( a – b ), BH = b

Hình vuông ABCD có diện tích bằng $a^2$

Hình vuông DKFG có diện tích bằng ${\left(a-b\right)}^2$

Hình chữ nhật AEFK có diện tích bằng ( a – b ) b

Hình vuông EBHF có diện tích bằng $b^2$

Hình chữ nhật HCGF có diện tích bằng ( a – b ).b

$S_{ABCD}=S_{DKFG}+S_{AEFK}=S_{EBHF}+S_{HCGF}$

nên ${\left(a-b\right)}^2+\left(a-b\right)b+\left(a-b\right)b+b^2=a^2$

⇒${\left(a-b\right)}^2=a^2-2ab+b^2$