Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải Sách Bài Tập Toán 8 Tập 1 !!
Qua tâm O của hình vuông ABCD cạnh a, kẻ...
Qua tâm O của hình vuông ABCD cạnh a, kẻ đường thắng l cắt cạnh AB
Câu hỏi :
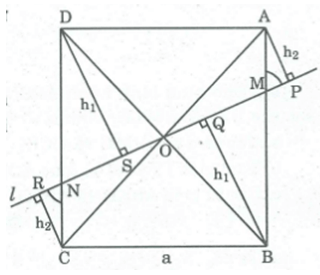
Qua tâm O của hình vuông ABCD cạnh a, kẻ đường thắng l cắt cạnh AB và CD lần lượt tại M và N. Biết MN = b. Hãy tính tổng các khoảng cách từ các đỉnh của hình vuông đến đường thẳng l theo a và b (a và b có cùng đơn vị đo).
* Đáp án
* Hướng dẫn giải
Gọi và là khoảng cách từ đỉnh B và đỉnh A đến đường thẳng l
Tổng khoảng cách là S.
Vì O là tâm đối xứng của hình vuông nên OM = ON (tính chất đối xứng tâm)
Suy ra AM = CN
Mà: (AMP) = (DNS) (đồng vị)
(DNS) = (CNR) (đôi đỉnh)
Suy ra: (AMP) = (CNR)
Suy ra: APM = CRN (cạnh huyền, góc nhọn)
⇒ CR = AP =
AM = CN ⇒ BM = DR
(BMQ) = (DNS) (so le trong)
Suy ra: BQM = DSN (cạnh huyền, góc nhọn) ⇒ DS = BQ =
(l)
= 1/2 .b/2 . + 1/2 .b/2 .
Từ (1) và (2) suy ra + = b . Vậy : S = 2( + ) = 2b
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Số câu hỏi: 794
Copyright © 2021 HOCTAP247